1.1.3. Мощность множества
Интуиция подсказывает, что термин мощность характеризует размер множества, а именно количество его элементов. И интуиция нас обманывает!
Мощность пустого множества равна нулю.
Мощность множества 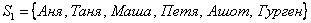 равна шести. равна шести.
Мощность множества букв русского алфавита 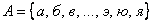 равна 33. равна 33.
И вообще – мощность любого конечного множества равно количеству элементов данного множества. …Возможно, не все до конца понимают, что такое конечное множество – если начать пересчитывать элементы этого множества, то рано или поздно счёт завершится. И китайцы тоже когда-нибудь закончатся, …в хорошем смысле :).
Само собой, множества можно сравнивать по мощности и их равенство в этом смысле называется равномощностью: два множества являются равномощными, если между ними можно установить взаимно-однозначное соответствие.
Множество 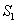 студентов равномощно множеству студентов равномощно множеству 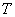 тем рефератов, которые я выдам вам в ближайшее время; множество тем рефератов, которые я выдам вам в ближайшее время; множество 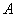 букв русского алфавита равномощно любому множеству из 33 элементов и т. д. Заметьте, что именно любому – в данном случае имеет значение лишь количество элементов. Буквы русского алфавита можно сопоставить не только с множеством номеров 1, 2, 3, …, 32, 33, но и вообще со стадом в 33 коровы. букв русского алфавита равномощно любому множеству из 33 элементов и т. д. Заметьте, что именно любому – в данном случае имеет значение лишь количество элементов. Буквы русского алфавита можно сопоставить не только с множеством номеров 1, 2, 3, …, 32, 33, но и вообще со стадом в 33 коровы.
Но гораздо более интересно обстоят дела с бесконечными множествами. Бесконечности тоже бывают разными! Зелёными и красными. Самые «маленькие» бесконечные множества – это счётные множества. Если совсем просто, элементы такого множества можно пронумеровать. Эталонный пример – это множество натуральных чисел 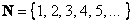 . Да – оно бесконечно, однако у каждого его элемента есть номер. . Да – оно бесконечно, однако у каждого его элемента есть номер.
Примеров много. В частности, счётным является множество всех чётных натуральных чисел 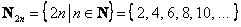 . Как это доказать? Нужно установить его взаимно-однозначное соответствие с множеством натуральных чисел или попросту пронумеровывать элементы: . Как это доказать? Нужно установить его взаимно-однозначное соответствие с множеством натуральных чисел или попросту пронумеровывать элементы:

Взаимно-однозначное соответствие установлено, следовательно, множества равномощны и множество 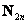 счётно. Парадоксально, но с точки зрения мощности, чётных натуральных чисел столько же – сколько и натуральных! счётно. Парадоксально, но с точки зрения мощности, чётных натуральных чисел столько же – сколько и натуральных!
Множество целых чисел счётно. Его элементы можно занумеровать, например, так:
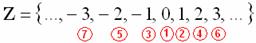
Более того, счётно и множество рациональных чисел 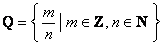 . Поскольку числитель – это целое число (а их, как только что показано, можно пронумеровать), а знаменатель – натуральное число, то рано или поздно мы «доберёмся» до любой рациональной дроби . Поскольку числитель – это целое число (а их, как только что показано, можно пронумеровать), а знаменатель – натуральное число, то рано или поздно мы «доберёмся» до любой рациональной дроби 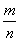 и присвоим ей номер. и присвоим ей номер.
А вот множество действительных чисел 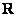 уже несчётно, т. е. его элементы пронумеровать невозможно. Этот факт строго доказан в теории множеств. Мощность множества действительных чисел также называют континуумом, и по сравнению со счётными множествами это «более бесконечное» множество. уже несчётно, т. е. его элементы пронумеровать невозможно. Этот факт строго доказан в теории множеств. Мощность множества действительных чисел также называют континуумом, и по сравнению со счётными множествами это «более бесконечное» множество.
Так как между множеством  и числовой прямой есть взаимно-однозначное соответствие, то множество точек числовой прямой тоже несчётно. И более того – что километровом, что миллиметровом отрезке точек столько же! Классический пример: и числовой прямой есть взаимно-однозначное соответствие, то множество точек числовой прямой тоже несчётно. И более того – что километровом, что миллиметровом отрезке точек столько же! Классический пример:
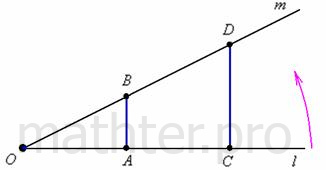
Поворачивая луч 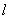 против часовой стрелки до его совмещения с лучом против часовой стрелки до его совмещения с лучом 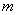 мы установим взаимно-однозначное соответствие между точками синих отрезков. Таким образом, на отрезке мы установим взаимно-однозначное соответствие между точками синих отрезков. Таким образом, на отрезке 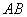 столько же точек, сколько и на отрезке и столько же точек, сколько и на отрезке и 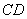 ! Этот парадокс, видимо, связан с загадкой бесконечности…, но мы сейчас не будем забивать голову проблемами мироздания, ибо на очереди тема, дух которых уже витает в воздухе: ! Этот парадокс, видимо, связан с загадкой бесконечности…, но мы сейчас не будем забивать голову проблемами мироздания, ибо на очереди тема, дух которых уже витает в воздухе:
 1.1.4. Операции (действия) с множествами 1.1.4. Операции (действия) с множествами
 1.1.2. Числовые множества 1.1.2. Числовые множества
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих
 1.1.4. Операции (действия) с множествами
1.1.4. Операции (действия) с множествами 1.1.2. Числовые множества
1.1.2. Числовые множества