2. Комплексные числа
Продолжаем разрабатывать тему числовых множеств. И прежде чем мы перейдем к рассмотрению комплЕксных чисел, дам важный совет: не пытайтесь представить их «в жизни» – это всё равно, что пытаться представить четвёртое измерение в нашем трёхмерном пространстве. Если хотите, комплексное число – это двумерное число.
Комплексным числом 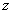 называется число вида называется число вида 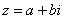 , где , где 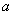 и и 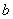 – действительные числа, – действительные числа, 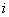 – так называемая мнимая единица. Число – так называемая мнимая единица. Число 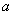 называется действительной частью ( называется действительной частью (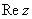 ) комплексного числа ) комплексного числа 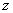 , а число , а число 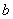 – мнимой частью ( – мнимой частью (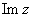 ) комплексного числа ) комплексного числа 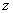 . .
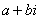 – это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: – это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: 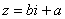 или переставить мнимую единицу: или переставить мнимую единицу: 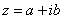 – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: 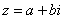 . Такую запись называют алгебраической формой комплексного числа. . Такую запись называют алгебраической формой комплексного числа.
И сразу отвечу на философский вопрос: зачем нужны комплексные числа? Всё очень просто. Эти числа появились исторически – в ходе развития математики, когда для решения некоторых задач стало не хватать действительных чисел.
Множество комплексных чисел обозначают стилизованной или жирной буквой 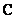 и изображают комплексной плоскостью, которая состоит из начала координат, действительной оси и изображают комплексной плоскостью, которая состоит из начала координат, действительной оси 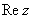 и мнимой оси и мнимой оси 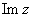 : :

На всякий пожарный напомню культуру построения чертежей: чтобы задать размерность, достаточно указать ноль, единицу на действительной оси и мнимую единицу 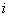 на мнимой оси. Не нужно проставлять значения «сплошняком»: …–3, –2, –1, 0, 1, 2, 3,… и на мнимой оси. Не нужно проставлять значения «сплошняком»: …–3, –2, –1, 0, 1, 2, 3,… и 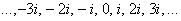 . Ибо (повторю свою бородатую шутку), комплексная плоскость – не памятник Эйлеру, а студент – не голубь. Впрочем, комплексные числа ввёл в обиход вовсе не Эйлер, и мы возвращаемся в теме: . Ибо (повторю свою бородатую шутку), комплексная плоскость – не памятник Эйлеру, а студент – не голубь. Впрочем, комплексные числа ввёл в обиход вовсе не Эйлер, и мы возвращаемся в теме:
Каждой точке комплексной плоскости соответствует некоторое комплексное число 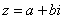 и наоборот, каждому комплексному числу соответствует своя точка плоскости. и наоборот, каждому комплексному числу соответствует своя точка плоскости.
Да чего тут мелочиться, рассмотрим чисел десять. Построим на комплексной плоскости следующие числа:
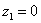 , , 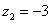 , , 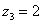
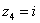 , , 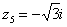 , , 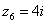
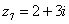 , , 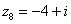 , , 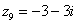 , , 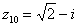
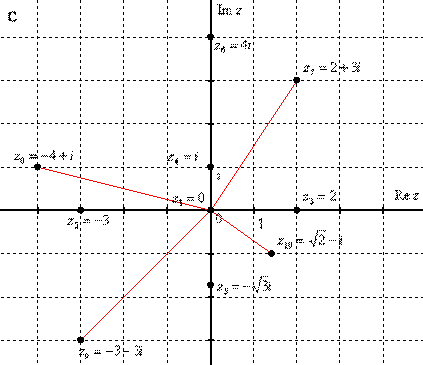
По какому принципу отмечены числа, думаю, всем видно – комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии.
Рассмотрим следующие комплексные числа: 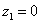 , , 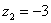 , , 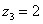 . Вы скажете: «Да это же это обыкновенные действительные числа!». И будете правы. Действительные числа – это частный случай комплексных чисел, и на действительной оси . Вы скажете: «Да это же это обыкновенные действительные числа!». И будете правы. Действительные числа – это частный случай комплексных чисел, и на действительной оси 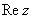 «сидят» все наши «обычные» числа. Таким образом, множество действительных чисел – это подмножество множества комплексных чисел «сидят» все наши «обычные» числа. Таким образом, множество действительных чисел – это подмножество множества комплексных чисел 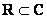 . .
Итак, числа 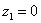 , , 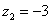 , , 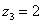 – это комплексные числа с нулевой мнимой частью. В частности, начало координат – есть число – это комплексные числа с нулевой мнимой частью. В частности, начало координат – есть число 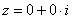 . .
Числа 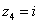 , , 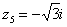 , , 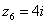 – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси  . .
В числах 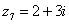 , , 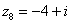 , , 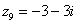 , , 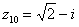 и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом). Радиус-векторы к числам, которые располагаются на осях, обычно не рисуют, по той причине, что они сливаются с осями. и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом). Радиус-векторы к числам, которые располагаются на осях, обычно не рисуют, по той причине, что они сливаются с осями.
На множестве комплексных чисел нет отношения порядка. Иными словами, комплексные числа невозможно сравнить другу с другом по принципу «больше / меньше» – для них такого понятия просто не существует. А вот понятие равенства есть: два комплексных числа равны, если равны их действительные и их мнимые части соответственно.
 2.1. Арифметические действия с комплексными числами 2.1. Арифметические действия с комплексными числами
 1.3. Понятие алгебраической структуры. Примеры 1.3. Понятие алгебраической структуры. Примеры
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих

 2.1. Арифметические действия с комплексными числами
2.1. Арифметические действия с комплексными числами 1.3. Понятие алгебраической структуры. Примеры
1.3. Понятие алгебраической структуры. Примеры