1.3. Понятие алгебраической структуры. Примеры
В этом небольшом параграфе я постараюсь заинтересовать читателя теоретической алгеброй, а если и нет – то Вы узнаете много важных и умных
слов, которые неоднократно встретятся в будущем :) И начнём мы не с алгебраических структур, а ни много ни мало, со
вселенских. Получится у меня не слишком научно, не слишком корректно, но для лучшего понимания – самое то. Итак, рассмотрим понятие
структуры, которая характеризуется следующими атрибутами:
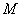 – непустое множество элементов; – непустое множество элементов;
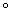 – некое действие с элементами множества или
какое-то их свойство; – некое действие с элементами множества или
какое-то их свойство;
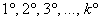 – набор аксиом ( – набор аксиом (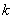 штук), которым удовлетворяет каждый элемент множества, а также заданная операция (либо свойство) штук), которым удовлетворяет каждый элемент множества, а также заданная операция (либо свойство) 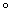 . .
В качестве примера рассмотрим структуру с условным называнием Объекты:
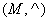 , где , где 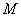 – произвольное непустое множество объектов окружающего мира, ^ – операция перемещения
в пространстве; при этом каждый элемент множества удовлетворяет следующей аксиоме: – произвольное непустое множество объектов окружающего мира, ^ – операция перемещения
в пространстве; при этом каждый элемент множества удовлетворяет следующей аксиоме: 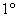 Обладание массой. Обладание массой.
Совершенно понятно, что этой структуре соответствует огромное количество множеств, поскольку во Вселенной двигается практически
всё :) Важным моментом является тот факт, что вместо перемещения можно рассматривать и другие действия (либо свойства) в рамках этой
структуры, например: @ – способность менять форму, # – способность менять агрегатное состояние (твёрдое тело / жидкость / газ) и
так далее. Важно, чтобы во всех случаях была выполнена аксиома 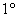 . .
Теперь рассмотрим структуру, которую назовём Путешественники:
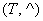 , где , где 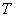 – непустое множество объектов окружающего мира, ^ – перемещение в пространстве, при
этом все элементы множества удовлетворяют следующим аксиомам: – непустое множество объектов окружающего мира, ^ – перемещение в пространстве, при
этом все элементы множества удовлетворяют следующим аксиомам:
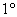 Обладание массой, Обладание массой, 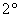 Способность вернуться в исходную точку пространства. Способность вернуться в исходную точку пространства.
Примеров здесь намного меньше, но всё равно много:
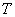 – исправный робот-пылесос (да, множество может
состоять из 1 элемента); – исправный робот-пылесос (да, множество может
состоять из 1 элемента);
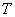 – множество студентов аудитории (которые способны,
например, выйти на перемену, а затем занять свои места); – множество студентов аудитории (которые способны,
например, выйти на перемену, а затем занять свои места);
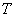 – множество планет Солнечной системы, и так
далее. – множество планет Солнечной системы, и так
далее.
А вот множество брошенных камней или молекулы жидкости в реке уже не обладает структурой Путешественники.
Разумеется, на множестве может быть задано бОльшее количество операций, рассмотрим структуру Светила:
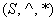 , где , где 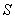 – непустое множество объектов окружающего мира, ^ – перемещение в пространстве, * –
способность излучать свет, при этом каждый элемент множества должен удовлетворять следующим аксиомам: – непустое множество объектов окружающего мира, ^ – перемещение в пространстве, * –
способность излучать свет, при этом каждый элемент множества должен удовлетворять следующим аксиомам: 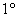 Обладание массой, Обладание массой, 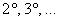 – аксиомы, связанные с излучением света. Подумайте, какие есть примеры кроме Солнца! – аксиомы, связанные с излучением света. Подумайте, какие есть примеры кроме Солнца!
И ключевой вопрос: зачем это всё нужно? Не только для классификации! Представьте, что мы изучаем некое множество и
выяснили (проверили аксиомы), что оно обладает структурой Путешественники. Но эта структура уже исследована в теории вдоль и
поперёк! Таким образом, мы сразу узнаЁм кучу характеристик и свойств этого множества!
…Надеюсь, у вас не взорвался мозг от моего творчества :) и хватит сил освоить алгебраические структуры. Такая структура состоит
из тех же атрибутов:
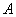 – непустое множество элементов; – непустое множество элементов;
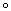 – бинарная операция с элементами множества; – бинарная операция с элементами множества;
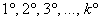 – набор аксиом, которым удовлетворяют все
элементы множества относительно заданной операции. – набор аксиом, которым удовлетворяют все
элементы множества относительно заданной операции.
Что значит бинарная? Это операция, когда мы берём два элемента множества, применяем к ней эту самую операцию и получаем один элемент, который принадлежит тому же самому множеству. Так, операция логического
отрицания бинарной не является, поскольку применяется к одному (а не к двум) элементам. Для множества натуральных чисел бинарно, в частности, сложение, ибо складывая два числа, мы
получаем одно значение, причём непременно натуральное. А вот операция вычитания на множестве  уже не бинарна, так как её результат – не обязательно натуральное число. Но зато
вычитание – есть бинарная операция на множестве уже не бинарна, так как её результат – не обязательно натуральное число. Но зато
вычитание – есть бинарная операция на множестве 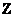 целых
чисел. целых
чисел.
Теперь я перечислю основные алгебраические структуры и приведу популярные примеры. Начнём с обширной структуры под называнием
Полугруппа:
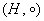 , где , где 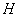 – непустое множество элементов, – непустое множество элементов, 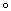 – бинарная операция на данном множестве, при этом выполнена аксиома ассоциативности операции: – бинарная операция на данном множестве, при этом выполнена аксиома ассоциативности операции:
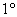 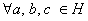 – для любых элементов «а», «бэ», «цэ» (проговариваем
вслух!!), принадлежащих множеству «аш», не имеет значения, в каком порядке будет выполнена цепочка операций: – для любых элементов «а», «бэ», «цэ» (проговариваем
вслух!!), принадлежащих множеству «аш», не имеет значения, в каком порядке будет выполнена цепочка операций: 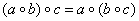 . .
В школе это называется сочетательным свойством, и напрашивающиеся примеры:
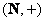 – множество натуральных чисел относительно сложения.
Совершенно понятно, что в любой сумме трёх натуральных чисел, без разницы, как мы расставим скобки: – множество натуральных чисел относительно сложения.
Совершенно понятно, что в любой сумме трёх натуральных чисел, без разницы, как мы расставим скобки: 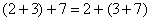 . Проверка: . Проверка:
слева 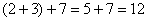 и справа: и справа: 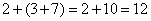
Результаты совпали, что и требовалось проверить. Да, алгебра тоже нещадно формальна! Как сказали бы древние римляне, Dura
algebra sed algebra =)
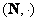 – множество натуральных чисел относительно умножения
– есть тоже, очевидно, полугруппа, ибо – множество натуральных чисел относительно умножения
– есть тоже, очевидно, полугруппа, ибо 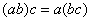 – для любых
натуральных значений. – для любых
натуральных значений.
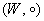 – множество – множество  слов (буквосочетаний) русского алфавита относительно операции слов (буквосочетаний) русского алфавита относительно операции  – «склеивания». Самостоятельно придумайте три слова и «склейте» их так: – «склеивания». Самостоятельно придумайте три слова и «склейте» их так: 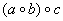 и в таком порядке: и в таком порядке: 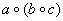 . …Очень хочется привести яркий пример, но в голову приходит то пошлятина какая-то, то унылый
«мосгортрест» :D . …Очень хочется привести яркий пример, но в голову приходит то пошлятина какая-то, то унылый
«мосгортрест» :D
Несмотря на кажущуюся «естественность», свойство ассоциативности выполнено далеко не всегда:
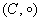 – множество – множество 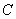 химических элементов относительно операции химических элементов относительно операции 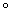 их соединения полугруппой не является, так как в общем случае их соединения полугруппой не является, так как в общем случае 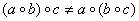 . Совершенно понятно, что в результате реакции . Совершенно понятно, что в результате реакции 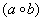 может получиться один химический элемент, а в результате может получиться один химический элемент, а в результате 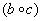 – совершенно другой. Вплоть до того, что в левой цепочке реакций получится по итогу конфетка, а в
правой – яд. – совершенно другой. Вплоть до того, что в левой цепочке реакций получится по итогу конфетка, а в
правой – яд.
Следующая структура – группа:
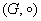 , где , где 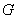 – непустое множество элементов, – непустое множество элементов,  – бинарная операция на данном множестве, для всех элементов
которого выполнены следующие три аксиомы: – бинарная операция на данном множестве, для всех элементов
которого выполнены следующие три аксиомы:
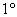 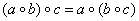 – ассоциативность операции, то есть любая группа является и полугруппой; – ассоциативность операции, то есть любая группа является и полугруппой;
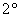 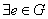 – существование нейтрального элемента, принадлежащего группе, такого, что – существование нейтрального элемента, принадлежащего группе, такого, что 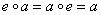 ; ;
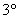 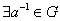 – существования обратного элемента, такого, что – существования обратного элемента, такого, что 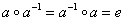 , ,
и если, кроме того, выполнена аксиома коммутативности операции:
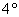 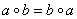
то группу называют коммутативной или абелевой группой.
Причём равенства 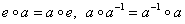 во 2-й и 3-й аксиомах – это не
пустая формальность, существуют алгебраические структуры, где они не выполняются. Аналогично аксиома 4 – хоть и кажется «незыблемой», но
есть структуры, где она не работает, и с некоторыми некоммутативными группами мы встретимся в настоящем курсе. во 2-й и 3-й аксиомах – это не
пустая формальность, существуют алгебраические структуры, где они не выполняются. Аналогично аксиома 4 – хоть и кажется «незыблемой», но
есть структуры, где она не работает, и с некоторыми некоммутативными группами мы встретимся в настоящем курсе.
Пример: 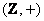 – множество
целых чисел относительно сложения является коммутативной группой, с нейтральным элементом – нулём: – множество
целых чисел относительно сложения является коммутативной группой, с нейтральным элементом – нулём: 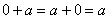 , а роль обратного элемента играет противоположное число: , а роль обратного элемента играет противоположное число: 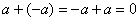 . .
Другой пример группы: 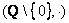 – множество рациональных чисел без нуля относительно умножения. Здесь нейтральный элемент – единица: – множество рациональных чисел без нуля относительно умножения. Здесь нейтральный элемент – единица: 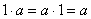 и обратный элемент и обратный элемент 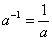 , для которого, очевидно, справедливо , для которого, очевидно, справедливо 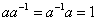 . .
Существует великое множество групп с конечным количеством элементов, тривиальные образцы: 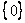 – множество, состоящее из одного нуля, относительно
операции сложения; – множество, состоящее из одного нуля, относительно
операции сложения; 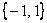 – множество из «плюс» и «минус»
единицы относительно умножения. – множество из «плюс» и «минус»
единицы относительно умножения.
Аксиомы проверьте самостоятельно!
И важный факт: элементы множества не обязаны быть числами, это могут быть векторы, матрицы, многочлены, функции, геометрические фигуры, а
то и вовсе нематематические объекты, как в примерах с полугруппами. С другой стороны, и операция 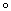 – не обязательно арифметическая, в частности, это может быть некоторое
функциональное или геометрическое преобразование. Важно, чтобы выполнялись аксиомы группы! Даже некоторые игры имеют структуру группы. – не обязательно арифметическая, в частности, это может быть некоторое
функциональное или геометрическое преобразование. Важно, чтобы выполнялись аксиомы группы! Даже некоторые игры имеют структуру группы.
Хорошо знакомыми примерам групп является следующие: 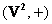 –
множество двумерных векторов относительно сложения и –
множество двумерных векторов относительно сложения и 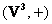 – и
множество трёхмерных векторов относительно той же операции. …Скорее всего, вам пришли в голову геометрические векторы, но на самом деле это
понятие шире, и позже я познакомлю вас с общим алгебраическим определением вектора. Ну а
сейчас маленькое задание для неофитов теории: – и
множество трёхмерных векторов относительно той же операции. …Скорее всего, вам пришли в голову геометрические векторы, но на самом деле это
понятие шире, и позже я познакомлю вас с общим алгебраическим определением вектора. Ну а
сейчас маленькое задание для неофитов теории:
Задача 3
Доказать, что множество векторов 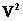 с действительными координатами – есть группа относительно сложения. с действительными координатами – есть группа относительно сложения.
Следующая структура – кольцо:
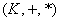 – есть множество – есть множество 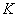 , на котором определены операции сложения и умножения и для всех элементов выполнены следующие
аксиомы: , на котором определены операции сложения и умножения и для всех элементов выполнены следующие
аксиомы:
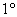 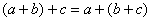 – – ассоциативность сложения; – – ассоциативность сложения;
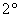 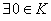 – существование нейтрального элемента («нуля») относительно сложения: – существование нейтрального элемента («нуля») относительно сложения: 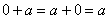 . .
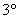 Для любого элемента Для любого элемента 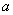 кольца кольца 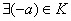 – существует противоположный (обратный относительно сложения) элемент: – существует противоположный (обратный относительно сложения) элемент: 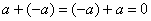 ; ;
 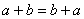 – коммутативность сложения. – коммутативность сложения.
Таким образом, кольцо является абелевой группой относительно сложения, но это ещё не всё:
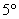 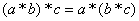 – ассоциативность умножения; – ассоциативность умножения;
 Свойства дистрибутивности: Свойства дистрибутивности:
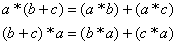
Попросту говоря, это раскрытие скобок. И многие кольца (а это уже кольцо) обладают нейтральным элементом относительно умножения
(«единицей»):
 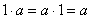
а также
 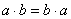 коммутативностью умножения. коммутативностью умножения.
«Эталонный» пример: множество целых чисел 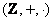 – есть коммутативное (относительно умножения) кольцо с единицей. А вот множество – есть коммутативное (относительно умножения) кольцо с единицей. А вот множество 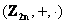 чётных целых чисел – тоже коммутативное кольцо, но уже без
единицы. чётных целых чисел – тоже коммутативное кольцо, но уже без
единицы.
Следует заметить, что структура кольцо – это уже ярко «арифметическая» структура (по сравнению с предыдущими), однако элементы
кольца могут быть не только числами, но и другими объектами, которые тоже можно складывать и умножать, правда, специфичным образом. Там
существуют свои особые нулевые и единичные элементы, именно поэтому я заключил в скобки «ноль» и «единицу» при перечислении аксиом. И
примеры таких колец будут в книге!
Далее, и, наконец. Если к аксиомам кольца добавить ещё одну:
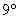 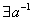 – существование обратного элемента относительно умножения, для всех ненулевых – существование обратного элемента относительно умножения, для всех ненулевых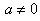 элементов множества: элементов множества: 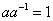 , ,
то получится алгебраическая структура под названием поле:
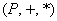
«Классические» примеры: поле рациональных чисел, поле действительных чисел и прямо сейчас мы переходим на поле
комплексных чисел.
Надеюсь, я кого-то заинтересовал теоретической алгеброй, и вы уже почувствовали её леденящий холодок :) Желающие могут найти тонны
литературы по самым разным аспектам предмета, в том числе структурам (коих гораздо больше, и не только алгебраических), ну а мы
начинаем нарабатывать практику
 2. Комплексные числа 2. Комплексные числа
 1.2.8. Эквиваленция. Необходимое и достаточное условие 1.2.8. Эквиваленция. Необходимое и достаточное условие
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих 2. Комплексные числа
2. Комплексные числа 1.2.8. Эквиваленция. Необходимое и достаточное условие
1.2.8. Эквиваленция. Необходимое и достаточное условие