6. Векторные пространства и линейные преобразования
Я так чувствую, вы соскучилась по теории, и поэтому в начале этой главы познакомимся с ещё одной, важнейшей алгебраической структурой и одним из центральных понятий математики:
6.1. Векторное (линейное) пространство. Так что же такое вектор?
До сих пор многие из вас представляют векторы лишь в их геометрическом смысле, но на самом деле это понятие гораздо шире.
Рассмотрим непустое множество 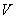 , для всех элементов которого определена операция сложения , для всех элементов которого определена операция сложения 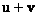 и операция умножения и операция умножения 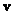 на на 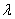 – элемент поля – элемент поля 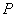 (чаще всего действительное число). При этом результаты операций: (чаще всего действительное число). При этом результаты операций: 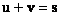 и и 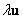 – тоже принадлежат множеству – тоже принадлежат множеству 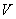 . …Всё понятно? ;) Вдумчиво перечитайте ещё раз! . …Всё понятно? ;) Вдумчиво перечитайте ещё раз!
Чтобы не путаться, элементы множества 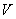 будем обозначать жирными буквами, а скаляры поля будем обозначать жирными буквами, а скаляры поля 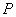 (числа) – нежирными и для надёжности ещё и греческими :). (числа) – нежирными и для надёжности ещё и греческими :).
Пусть для всех элементов множества 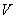 и всех элементов поля и всех элементов поля 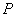 выполнены следующие аксиомы: выполнены следующие аксиомы:
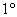 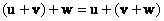 – ассоциативность сложения; – ассоциативность сложения;
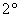 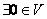 – существование нейтрального элемента («нуля») относительно сложения – существование нейтрального элемента («нуля») относительно сложения 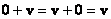 ; ;
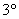 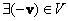 – существования обратного элемента относительно сложения, то есть противоположного элемента, такого, что – существования обратного элемента относительно сложения, то есть противоположного элемента, такого, что 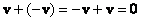 ; ;
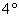 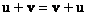 – коммутативность сложения. – коммутативность сложения.
Заметьте, что это уже абелева группа. И кроме того:
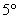 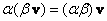 – ассоциативность умножения на скаляр; – ассоциативность умножения на скаляр;
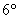 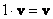 – унитарность (умножение на единицу поля – унитарность (умножение на единицу поля 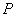 сохраняет элемент сохраняет элемент 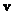 ); );
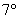 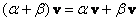 – дистрибутивность относительно суммы скаляров; – дистрибутивность относительно суммы скаляров;
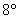 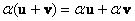 – дистрибутивность относительно суммы элементов множества – дистрибутивность относительно суммы элементов множества 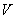 . .
Тогда (барабанная дробь!): множество 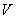 называют линейным или векторным пространством над полем называют линейным или векторным пространством над полем 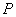 , а элементы множества , а элементы множества 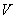 – векторами. – векторами.
Кратко сия алгебраическая структура обозначается через 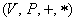 , а векторы – либо с привычными черточками наверху , а векторы – либо с привычными черточками наверху 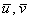 либо жирными латинскими буквами либо жирными латинскими буквами 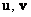 (характерно для литературы), дабы отличать их от других объектов. (характерно для литературы), дабы отличать их от других объектов.
Запишем известные нам геометрические векторные пространства:
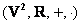 – множество двумерных векторов с операциями сложения векторов и умножения вектора на действительное число; – множество двумерных векторов с операциями сложения векторов и умножения вектора на действительное число;
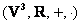 – аналогичное множество трёхмерных векторов нашего пространства. – аналогичное множество трёхмерных векторов нашего пространства.
Самостоятельно убедИтесь в справедливости вышеизложенных утверждений и выполнении всех аксиом векторого пространства (проще всего, координатным методом).
Но геометрические векторы – это лишь частный случай! Существует много векторных пространств, не имеющих отношения к геометрии! ВажнО лишь формальное выполнение определения (в том числе аксиом) векторного пространства – и тогда рассматриваемое множество будет векторным пространством, а его элементы – векторами. Даже если это множество медведей на велосипеде. Но давайте начнём с мАлого :).
Прежде всего, Задание: кратко сформулируйте определение векторного пространства 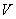 над полем действительных чисел. А то я меня как-то получилось длинно:) над полем действительных чисел. А то я меня как-то получилось длинно:)
Выполняем письменно! – и заметьте, это уже не общее определение, здесь есть конкретика ;) Свериться можно в конце книги (после решения Примера 128), и далее по умолчанию (если не сказано иного) будем рассматривать именно такие пространства.
И, конечно же, другие примеры! Их тьма, но я выберу самый свет :)
Рассмотрим упорядоченную строку (или столбец, не принципиально) произвольных действительных чисел 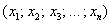 . Множество таких строк с заданной операцией их сложения . Множество таких строк с заданной операцией их сложения 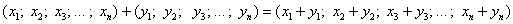 и умножения на вещественное число и умножения на вещественное число 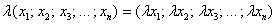 образует так называемое арифметическое векторное пространство образует так называемое арифметическое векторное пространство 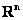 (читается «эр эн»). Объект (читается «эр эн»). Объект 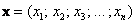 является вектором пространства является вектором пространства 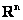 , а числа , а числа 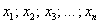 – его координатами. Нейтральный элемент пространства – есть нулевой вектор – его координатами. Нейтральный элемент пространства – есть нулевой вектор 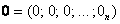 . .
В частности, если 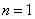 , то… получается множество действительных чисел , то… получается множество действительных чисел 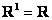 , которое оказывается векторным пространством! То есть вещественные числа можно считать одномерными векторами. При , которое оказывается векторным пространством! То есть вещественные числа можно считать одномерными векторами. При 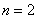 , , 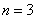 пространство «эр эн» тоже имеет геометрический смысл – известные нам «плоские» и пространственные векторы. Но, разумеется, числа в строках (либо столбцах) могут иметь самый разный смысл, вне зависимости от пространство «эр эн» тоже имеет геометрический смысл – известные нам «плоские» и пространственные векторы. Но, разумеется, числа в строках (либо столбцах) могут иметь самый разный смысл, вне зависимости от 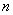 . .
Пример по горячим следам: множество частных решений системы однородных линейных уравнений (какой-то конкретной) образует векторное пространство. Так, в Примере 117 мы получили множество частных решений 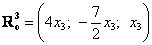 (свободная переменная (свободная переменная 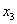 принимает все действительные значения). А, кстати, почему это векторное пространство? Ведь не всё так очевидно…. принимает все действительные значения). А, кстати, почему это векторное пространство? Ведь не всё так очевидно….
Во-первых, данное множество замкнуто относительно операции сложения и умножения на число. А именно, если сложить любые два частных решения, то в результате обязательно получится частное решение. И если любое частное решение умножить на произвольное вещественное число, то тоже – непременно получится частное решение данной системы. Предлагаю Вам строго обосновать эти факты (подсказка: подставьте сумму двух частных решений в левую часть каждого уравнения системы (Пример 117)).
И во-вторых, для множества 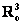 выполнены 8 аксиом линейного пространства – убедИтесь в этом опять же самостоятельно. выполнены 8 аксиом линейного пространства – убедИтесь в этом опять же самостоятельно.
Вывод: 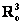 – векторное пространство, и здесь мы сталкиваемся ещё с одним понятием. Это пространство является подпространством арифметического пространства – векторное пространство, и здесь мы сталкиваемся ещё с одним понятием. Это пространство является подпространством арифметического пространства 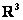 . Ну ещё бы – ведь множество . Ну ещё бы – ведь множество 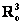 содержит лишь некоторые строки из трёх чисел. содержит лишь некоторые строки из трёх чисел.
Однако строже: непустое множество 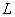 называется векторным подпространством векторного пространства называется векторным подпространством векторного пространства 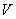 , если все элементы , если все элементы 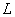 (в том числе нулевой) содержатся в (в том числе нулевой) содержатся в 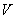 , и операции с ними замкнуты в «эль»: , и операции с ними замкнуты в «эль»: 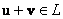 и и 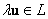 . .
Давайте теперь уберём знаки препинания:
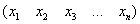
Что получилось? Получилась матрица «один на эн» или попросту строка. Множество строк фиксированной длины «эн» образует векторное пространство. И в самом деле – вспОмните правило сложения матриц и умножения матрицы на число. Аналогичное утверждение, разумеется, справедливо и для столбцов. По этой причине такие матрицы иногда называют вектором-строкой и вектор-столбцом.
И вообще, множество матриц фиксированного размера «эм на эн» 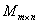 образует векторное пространство. Рекомендую взять конкретный размер, например, «два на три» и убедиться в замкнутости операций (впрочем, это очевидно) и выполнении 8 аксиом линейного пространства. Кстати, первые четыре мы уже проверили. образует векторное пространство. Рекомендую взять конкретный размер, например, «два на три» и убедиться в замкнутости операций (впрочем, это очевидно) и выполнении 8 аксиом линейного пространства. Кстати, первые четыре мы уже проверили.
Так вот оно как! – оказывается, матрицы – это тоже векторы!
И множество всех многочленов одной переменной – тоже векторное пространство! Проверьте данный факт самостоятельно. Можно взять какие-то конкретные многочлены и выполнить «прикидку», а можно выполнить проверку в общем виде, с этим кретиативным занятием я вас на всякий случай немного познакомил :)
Однако всегда нужно следить за контекстом. Так, множество многочленов 7-й (например) степени не образует векторное пространство. Почему? По той причине, что не всегда выполнена замкнутость сложения. Если, скажем, к многочлену 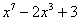 прибавить прибавить 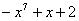 , то получится многочлен , то получится многочлен 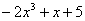 – третьей степени. Но, по определению векторного пространства (см. начало), сумма обязательно должна принадлежать тому же множеству. А вот если сказать «множество многочленов степени, мЕньшей семи» – то это уже линейное пространство. И многочлены 7-й степени сюда не входят! – третьей степени. Но, по определению векторного пространства (см. начало), сумма обязательно должна принадлежать тому же множеству. А вот если сказать «множество многочленов степени, мЕньшей семи» – то это уже линейное пространство. И многочлены 7-й степени сюда не входят!
Поэтому будьте внимательны! Пытливые преподаватели – пытать вас будут (^ ^)
Рассмотрим множество функций одной переменной, которые определены и непрерывны на всей числовой прямой (на 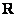 ). …Интуитивное понятие непрерывности, думаю, всем понятно: функция непрерывна на некотором промежутке, если её график можно нарисовать, не отрывая карандаша от бумаги. Кстати, давайте, ещё раз взглянем в Приложение К задаче 2 и вспомним, какие из элементарных функций непрерывны всюду. После чего вернёмся к теме и обозначим множество таких функций через ). …Интуитивное понятие непрерывности, думаю, всем понятно: функция непрерывна на некотором промежутке, если её график можно нарисовать, не отрывая карандаша от бумаги. Кстати, давайте, ещё раз взглянем в Приложение К задаче 2 и вспомним, какие из элементарных функций непрерывны всюду. После чего вернёмся к теме и обозначим множество таких функций через 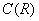 . .
По соответствующей теореме математического анализа, сумма двух непрерывных функций 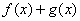 – есть функция непрерывная, и, очевидно, функция – есть функция непрерывная, и, очевидно, функция 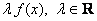 тоже непрерывна. То есть множество тоже непрерывна. То есть множество 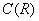 замкнуто относительно этих операций. Опираясь на теоретические выкладки матана и очевидные факты, нетрудно убедиться в справедливости 8 аксиом векторного пространства, где нулевой элемент – есть функция замкнуто относительно этих операций. Опираясь на теоретические выкладки матана и очевидные факты, нетрудно убедиться в справедливости 8 аксиом векторного пространства, где нулевой элемент – есть функция 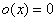 (ось (ось 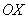 ), а противоположный – со знАком минус, ака ), а противоположный – со знАком минус, ака 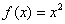 и и 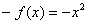 . .
Вывод: 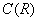 – векторное пространство. К слову, навеял тут «икс квадрат»: множество функций-многочленов – есть линейное подпространство пространства – векторное пространство. К слову, навеял тут «икс квадрат»: множество функций-многочленов – есть линейное подпространство пространства 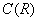 . .
Вместо числовой прямой можно рассмотреть конкретный отрезок, и множество функций 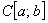 , непрерывных на данном отрезке – это тоже векторное пространство. Заметьте, что функций здесь прибавится, ибо тангенсы, логарифмы и иже с ними грешники – вполне себе непрерывны на многих отрезках. , непрерывных на данном отрезке – это тоже векторное пространство. Заметьте, что функций здесь прибавится, ибо тангенсы, логарифмы и иже с ними грешники – вполне себе непрерывны на многих отрезках.
Вот такие вот бывают векторы, о которых многие из вас даже не подозревали!
 6.2. Основные понятия векторного пространства 6.2. Основные понятия векторного пространства
 5.11. Как найти обратную матрицу методом элементарных преобразований? 5.11. Как найти обратную матрицу методом элементарных преобразований?
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих 6.2. Основные понятия векторного пространства
6.2. Основные понятия векторного пространства 5.11. Как найти обратную матрицу методом элементарных преобразований?
5.11. Как найти обратную матрицу методом элементарных преобразований?