4.10. Матрицы с точки зрения алгебраической структуры
Множество матриц фиксированного (жёстко заданного) размера «эм на эн» 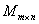 образует коммутативную группу относительно сложения. образует коммутативную группу относительно сложения.
Рассмотрим, например, множество матриц «два на три» 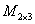 с операцией сложения и проверим аксиомы группы. Очевидно, для любых матриц с операцией сложения и проверим аксиомы группы. Очевидно, для любых матриц  , ,  , , 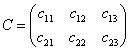 выполнена: выполнена:
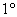 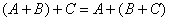 – аксиома ассоциативности сложения. Это элементарно проверяется с помощью правила сложения. – аксиома ассоциативности сложения. Это элементарно проверяется с помощью правила сложения.
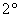 Среди множества матриц «два на три» существует нейтральный элемент Среди множества матриц «два на три» существует нейтральный элемент 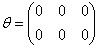 (нулевая матрица), такой, что: (нулевая матрица), такой, что: 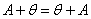 . .
 Для любой матрицы Для любой матрицы  существует обратный элемент, роль которого играет противоположная матрица существует обратный элемент, роль которого играет противоположная матрица 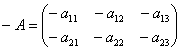 с очевидным фактом: с очевидным фактом: 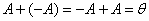 . .
 И, наконец, матрицы коммутативны по сложению: И, наконец, матрицы коммутативны по сложению: 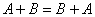 . Этот пункт мы неоднократно доказывали ранее: находим сумму левой части, находим сумму правой части и, пользуясь коммутативностью самих чисел, приходим к выводу, что левая часть равна правой. . Этот пункт мы неоднократно доказывали ранее: находим сумму левой части, находим сумму правой части и, пользуясь коммутативностью самих чисел, приходим к выводу, что левая часть равна правой.
Вывод: 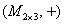 – абелева группа – абелева группа
Аналогично можно показать, что множество матриц 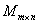 какого-то другого фиксированного размера тоже образует аддитивную группу (группу по сложению). Потихоньку нагружаю вас новыми терминами (^ ^). какого-то другого фиксированного размера тоже образует аддитивную группу (группу по сложению). Потихоньку нагружаю вас новыми терминами (^ ^).
Далее:
Множество невырожденных квадратных матриц фиксированного размера «эн на эн» 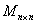 образует некоммутативную группу относительно умножения. Напоминаю, что матрица не вырождена, если её определитель отличен от нуля. образует некоммутативную группу относительно умножения. Напоминаю, что матрица не вырождена, если её определитель отличен от нуля.
Рассмотрим, например, множество невырожденных матриц «два на два» 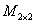 с операцией умножения и убедимся, что это группа. Для любых матриц с операцией умножения и убедимся, что это группа. Для любых матриц 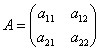 , , 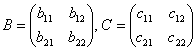 выполнена освещённая недавно ассоциативность умножения: выполнена освещённая недавно ассоциативность умножения:
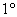 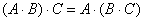 . Желающие могут строго проверить этот факт прямым перемножением матриц слева и справа, правда, выкладки будут весьма громоздкими. . Желающие могут строго проверить этот факт прямым перемножением матриц слева и справа, правда, выкладки будут весьма громоздкими.
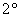 Среди множества матриц «два на два» существует нейтральный элемент, а именно единичная матрица Среди множества матриц «два на два» существует нейтральный элемент, а именно единичная матрица 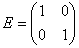 с опять же проверенным на практике свойством с опять же проверенным на практике свойством 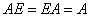 . .
 Для любой невырожденной матрицы Для любой невырожденной матрицы 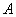 существует обратный элемент существует обратный элемент 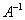 (обратная матрица), такой, что (обратная матрица), такой, что 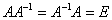 . .
И, как мы неоднократно видели ранее, умножение матриц в общем случае не перестановочно: 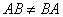 . .
Вывод: 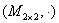 – некоммутативная группа. – некоммутативная группа.
Аналогично можно рассмотреть множество квадратных матриц какого-то другого фиксированного размера. Иногда группу относительно умножения называют мультипликативной. Но это ещё не всё!
Множество невырожденных квадратных матриц фиксированного размера «эн на эн» 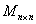 образует некоммутативное (относительно умножения) кольцо с «единицей». образует некоммутативное (относительно умножения) кольцо с «единицей».
Первые четыре аксиомы кольца, очевидно, выполнены (см. начало параграфа). Ассоциативность умножения (аксиома 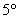 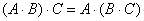 ) только что показана. А вот следующий факт – «новинка»: ) только что показана. А вот следующий факт – «новинка»:
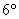 Для любых трёх квадратных матриц фиксированного размера выполнены свойства дистрибутивности: Для любых трёх квадратных матриц фиксированного размера выполнены свойства дистрибутивности: 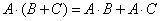 и и 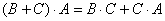 . Попросту говоря, у матриц, точно так же как у чисел, можно раскрывать скобки. Пользуйтесь на здоровье – в удобных случаях. . Попросту говоря, у матриц, точно так же как у чисел, можно раскрывать скобки. Пользуйтесь на здоровье – в удобных случаях.
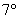 Существование обратного элемента тоже недавно показано: Существование обратного элемента тоже недавно показано: 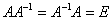 , но вот 8-я аксиома «подкачала», ибо матричное умножение некоммутативно. , но вот 8-я аксиома «подкачала», ибо матричное умножение некоммутативно.
Вывод: 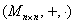 («эн» фиксировано) – некоммутативное кольцо с «единицей». («эн» фиксировано) – некоммутативное кольцо с «единицей».
Но и это ещё не всё! Есть ещё одна известная алгебраическая структура, с которой вы однозначно сталкивались, и которую я оставлю до следующей главы…. Ибо курс у нас больше практический, и мы продолжаем ему следовать:
 4.11. Некоторые полезные свойства определителей 4.11. Некоторые полезные свойства определителей
 4.9. Матричные выражения 4.9. Матричные выражения
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих ,
,  ,
, 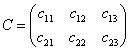 выполнена:
выполнена: существует обратный элемент, роль которого играет противоположная матрица
существует обратный элемент, роль которого играет противоположная матрица 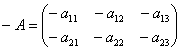 с очевидным фактом:
с очевидным фактом: 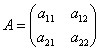 ,
, 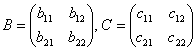 выполнена освещённая недавно
выполнена освещённая недавно  4.11. Некоторые полезные свойства определителей
4.11. Некоторые полезные свойства определителей 4.9. Матричные выражения
4.9. Матричные выражения