|
Ваш репетитор, справочник и друг!
|
4.11. Некоторые полезные свойства определителейКак и в случае с матричными операциями, у определителей насчитывается добрый десяток свойств, однако реальное прикладное значение имеют только некоторые из них. Но начать хочется с более насущного вопроса: 4.11.1. Золотое правило вычислений– поручить вычисления товарищу или компьютеру =) В данном пункте речь пойдёт о технике эффективного вычисления определителей, которая позволит вам находить их максимально быстро. Возможно, некоторые скажут: «ерунда, какая разница – потратим мы 2 минуты или 3?». Но это всё хорошо, если определитель не очень большой. А если «четыре на четыре»? А если «пять на пять»? Который, кстати, тоже встречается. Сидеть 10-20 минут, а то и дольше (в случае ошибки) что-то совсем неохота. Да и зачем 2-3 минуты сидеть? Не редкость, когда процесс решения вполне реально сократить до считанных секунд, а иногда и сразу увидеть результат! Чему и будет посвящён наш дальнейший разговор. Мотив рационального вычисления определителя встретился нам в первом же примере по теме: Да, разложить, определитель по 1-й строке или 1-му столбцу – это привычно и академично, но 2-я строка или 2-й столбец (где есть ноль) приводят к результату заметно быстрее. Давайте вспомним «любительскую» матрицу знаков Это быстрее чем, по 1-й строке? Конечно. Тем более, на практике нулевое слагаемое принято опускать: А если в строке или столбце два нуля, то это вообще настоящий подарок: Пример 69 Вычислить определитель матрицы Здесь два нуля в третьей строке, по ней и раскрываем: Особый случай, когда определитель имеет так называемый ступенчатый или треугольный вид, например: Разложим его по первому столбцу: В практических заданиях удобно руководствоваться следующим правилом – ступенчатый определитель равен произведению чисел его главной диагонали: Аналогичный принцип справедлив и для ступенчатых определителей других порядков, например: Треугольные определители иногда встречаются, и их решение лучше оформлять именно так! А если в строке (столбце) определителя находятся одни нули? Ответ, думаю, понятен. Впрочем, о нулевых определителях позже. Сейчас о другом: Пример 70
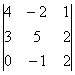
Здесь вообще нет нулей, но всё равно существует способ облегчить себе жизнь! Данный определитель выгоднее разложить по третьему столбцу, поскольку там самые маленькие числа. И запись принимает очень приятный вид: И, резюмируя параграф, сформулируем золотое правило вычислений: Определитель выгодно раскрывать по ТОЙ строке (или столбцу), где: 1) нулей побольше; И чем больше порядок определителя, тем больше вес золота. Самостоятельно: Пример 71 Вычислить определитель, используя наиболее рациональный способ
И ещё один важный совет: не комплексуйте! Не надо бояться показаться «слишком умным» и «зацикливаться» на традиционном разложении по первой строке либо первому столбцу. Как короче – так и решайте! Этой же цели служат некоторые правила, о которых я расскажу ниже:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих
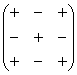 ,
, 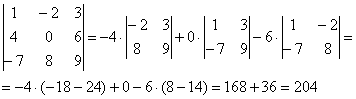
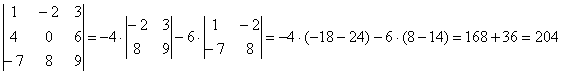

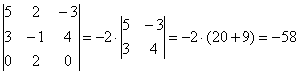
 – в таком определителе все числа, расположенные ниже главной диагонали, равны нулю.
– в таком определителе все числа, расположенные ниже главной диагонали, равны нулю.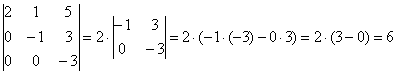
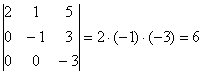
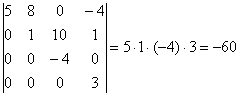
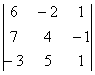
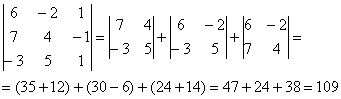
 4.11.2. Определитель транспонированной матрицы
4.11.2. Определитель транспонированной матрицы 4.10. Матрицы с точки зрения алгебраической структуры
4.10. Матрицы с точки зрения алгебраической структуры