|
Ваш репетитор, справочник и друг!
|
4.11.2. Определитель транспонированной матрицыРассмотрим старых знакомых: матрицу На всякий случай повторю элементарное различие между понятиями: матрица – это таблица элементов, а определитель – суть число (числа квадратной матрицы, с которыми нужно выполнить определённые действия и получить это самое число). При транспонировании матрицы определитель не меняется. Транспонируем матрицу: Согласно свойству, определитель транспонированной матрицы равен тому же значению: Запишем оба определителя рядышком и проанализируем один важный момент: В результате транспонирования первая строка стала первым столбцом, вторая строка – вторым столбцом, третья строка – третьим столбцом. Строки стали столбцами, а результат не изменился. Призрак этого факта давно бродит по страницам темы, и настал момент его озвучить: строки и столбцы определителя равноправны Иными словами, если какое-нибудь свойство справедливо для строк, то аналогичное свойство справедливо и для столбцов! И в действительности мы с этим уже сталкивались – ведь определитель можно раскрыть как по строке, так и равноправно по столбцу. Не нравятся числа в строках? Транспонируйте определитель! Подчёркиваю, что определитель. САМУ МАТРИЦУ просто так транспонировать нельзя!
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих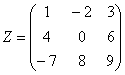 и её определитель
и её определитель 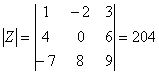 .
. 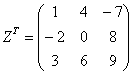
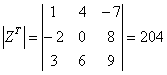 . Желающие могут убедиться в этом самостоятельно.
. Желающие могут убедиться в этом самостоятельно.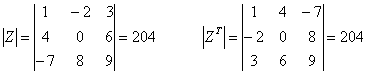
 4.11.3. Парная перестановка строк (столбцов)
4.11.3. Парная перестановка строк (столбцов) 4.11.1. Золотое правило вычисления определителей
4.11.1. Золотое правило вычисления определителей