4.8.3. Как перемножить три матрицы?

Произведение трёх матриц (если оно осуществимо) можно вычислить двумя способами:

1) найти , а затем домножить результат на матрицу «цэ»: ;

2) либо сначала найти и потом выполнить умножение .

Результаты обязательно совпадут, то есть матричное умножение, как и умножение обычных чисел, ассоциативно:

Пример 63

Перемножить матрицы двумя способами

Решение будет состоять из двух пунктов, причём в каждом из них два шага: находим произведение двух матриц, затем снова находим произведение двух матриц.

Способ первый:

1) Перемножим матрицы в следующем порядке:
Действие первое:

Действие второе:

И способ второй:

2) Выполним умножение так: .
Действие первое:

Действие второе:

Ответ:

Более привычен и стандартен, конечно же, первый способ решения, там «как бы всё по порядку». Кстати, по поводу порядка. В рассматриваемом задании часто возникает иллюзия, что речь идёт о каких-то перестановках матриц. Их здесь нет. Снова напоминаю, что в общем случае ПЕРЕСТАВЛЯТЬ МАТРИЦЫ НЕЛЬЗЯ. Так, во втором пункте на втором шаге выполняем умножение , но ни в коем случае не .

Свойство ассоциативности умножения справедливо не только для квадратных, но и для произвольных прямоугольных матриц – лишь бы они умножались:

Пример 64

Найти произведение трёх матриц

Это пример для самостоятельного решения. В образце решения (конец книги) вычисления проведены двумя способами, проанализируйте, какой путь выгоднее и короче.

Свойство ассоциативности матричного умножения справедливо и для бОльшего количества множителей, и живой тому пример встретится в следующем пункте:

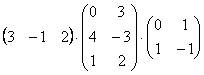
4.8.4. Как возвести матрицу в куб и более высокие степени?

4.8.2. Коммутативность числового множителя

| Оглавление |

Автор: Aлeксaндр Eмeлин