4.8.2. Коммутативность числового множителя

Напоминаю, что коммутативность – это перестановочность, и этим свойством мы уже пользовались, когда проверяли обратную матрицу. Для матриц и действительного числа справедливо следующее:

, то есть числовой множитель можно (и во многих случаях нужно) вынести вперёд, чтобы он не «мешался под ногами».

Пример 61

Вычислить произведение

В лучших своих традициях закомментирую каждый шаг решения:

(1) Согласно свойству перемещаем числовой множитель вперёд. Сами матрицы переставлять нельзя!

(2) – (3) Выполняем матричное умножение.

(4) Здесь можно поделить каждое число 10, но тогда среди элементов матрицы появятся десятичные дроби, что не есть хорошо. Однако замечаем, что все числа матрицы делятся на 5, поэтому умножаем каждый элемент на .

Окончательный ответ лучше оставить в виде , хотя, в принципе, годится и внесение дроби: .

Ответ:

Маленькая шарада для самостоятельного решения:

Пример 62

Вычислить , если

Здесь число (–1) вполне уместно сразу внести во 2-ю матрицу, но в своей версии решения я всё же этого не сделал, чтобы не плодить минусы в матрице .

Свойство коммутативности числового множителя, справедливо для любого количества умножаемых матриц, причём его можно поставить в любое место, да хоть в самый конец. Или умножить на любую матрицу, если это выгодно.

Следует отметить, что все эти свойства, даже очевидные, строго доказываются в теории, ибо «очевидное» может запросто оказаться ошибочным (припомним хотя бы «неочевидное» )

Прицепим к паровозику ещё один вагончик:

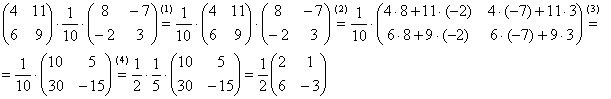
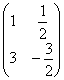4.8.3. Как перемножить три матрицы?

4.8.1. Как возвести матрицу в квадрат?

| Оглавление |

Автор: Aлeксaндр Eмeлин