|
Ваш репетитор, справочник и друг!
|
4.7. Обратная матрицаЧто такое обратная матрица? Тут можно провести аналогию с обратными числами: рассмотрим, например, оптимистичное число 5 и обратное ему
число С матрицами всё похоже! Произведение квадратной матрицы Понятие обратной матрицы вводится только для квадратных матриц: «два на два», «три на три» и т. д. Начнём с простейшего случая: Пример 58 Дана матрица Обратную матрицу можно найти с помощью элементарных преобразований (разберём позже), но гораздо чаще
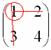
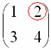
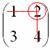
используют готовую формулу: Если Решение удобно оформить по пунктам: 1) Сначала находим определитель матрицы: 2) Находим матрицу миноров Матрица миноров имеет такие же размеры, как и матрица Как добывать миноры, мы только что разобрали, и поэтому секретов тут нет. Впрочем, ещё раз повторим, в картинках, так как среди моих читателей есть и дети. Сначала рассмотрим левый верхний элемент матрицы Как найти его минор? МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент: Рассматриваем следующий элемент матрицы Аналогично рассматриваем элементы второй строки и находим их миноры: Таким образом: 3) Находим матрицу алгебраических дополнений Поскольку В нашей задаче: 4) Находим транспонированную матрицу алгебраических дополнений То есть, строки матрицы 5) Собственно, ответ готов. По формуле: Обратную матрицу лучше оставить в таком виде. Делить каждый элемент матрицы на 2 не надо – по той причине, что получатся дробные числа. А оно зачем? Как проверить решение? Нужно выполнить матричное умножение Проверка: Ну, или наоборот, без разницы: Теперь переходим к более распространенному на практике случаю – «три на три»: Пример 59 Найти обратную матрицу для матрицы Алгоритм точно такой же, как и для матрицы «два на два». Решение: обратную матрицу найдем по формуле: 1) Вычислим определитель матрицы. Разложу его по первой
строке: 2) Находим матрицу миноров Матрица миноров имеет размерность «три на три» Рассмотрим левый верхний элемент матрицы: И для закрепления алгоритма – нахождение ещё одного минора в картинках: Как вы, наверное, догадались, здесь нужно вычислить девять определителей «два на два». Процесс, конечно, муторный, но случай не самый тяжелый, бывает хуже. Задание: вычислить (НА БУМАГЕ) остальные миноры. При чистовом оформлении примера лучше использовать «цивилизованные» обозначения: Миноры Итак, в результате вычислений у нас образовалась следующая матрица миноров: То, что все они получились отрицательными – чистая случайность. 3) Находим матрицу алгебраических дополнений Поскольку В нашей задаче: 4) Находим транспонированную матрицу алгебраических дополнений
5) Ответ: Теперь выполним проверку. Для этого нужно вычислить
Задание: выполнить матричное умножение Образец решения в конце книги (Пример 59). Как найти обратную матрицу для матрицы «четыре на четыре»? Там придётся вычислить 1 определитель «четыре на четыре» и 16 определителей «три на три». …Но то я, конечно, пошутил :) В тяжелых случаях целесообразно использовать метод элементарных преобразований. Хотя, на моей памяти был случай, когда студента заставили находить обратную матрицу «четыре на четыре» «каторжным» способом. И если вы окажетесь таким «счастливчиком», то минут так 40-50 это займёт, что ж поделать…. Ну а теперь переходим в «старшие классы» и продолжаем «набивать руку» на матрицах и определителях:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
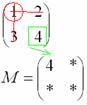
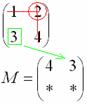
Высшая алгебра для начинающих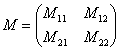 , для простоты обозначим неизвестные
звёздочками:
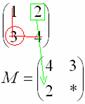
, для простоты обозначим неизвестные
звёздочками: 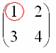
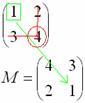
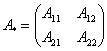 .
.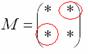
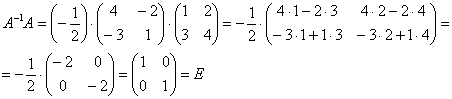
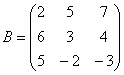
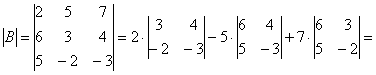
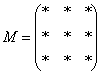 , и нам нужно найти девять чисел. Подробно распишу парочку миноров:
, и нам нужно найти девять чисел. Подробно распишу парочку миноров: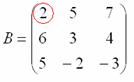
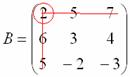
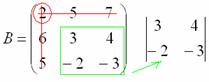
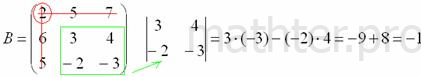
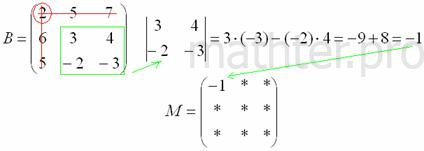
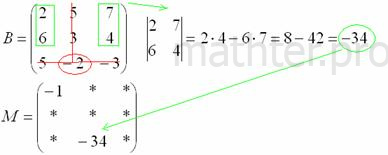
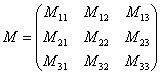
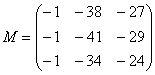
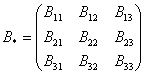 .
.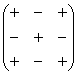 , то есть в матрице миноров
нужно сменить знаки у следующих чисел:
, то есть в матрице миноров
нужно сменить знаки у следующих чисел: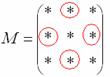
 – матрица алгебраических
дополнений соответствующих элементов матрицы
– матрица алгебраических
дополнений соответствующих элементов матрицы 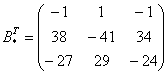 –
– 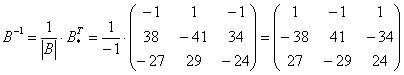 , тот редкий случай, когда обратная матрица получилась
«красивой».
, тот редкий случай, когда обратная матрица получилась
«красивой».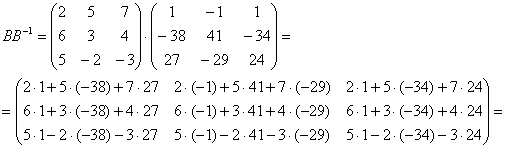
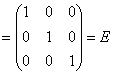 , значит, обратная матрица найдена правильно.
, значит, обратная матрица найдена правильно. 4.8. И снова о матричном умножении
4.8. И снова о матричном умножении 4.6. Миноры и алгебраические дополнения
4.6. Миноры и алгебраические дополнения