5.11. Как найти обратную матрицу методом Гаусса-Йордана?
Или методом Гаусса. Или с помощью элементарных преобразований. Или методом присоединённой матрицы. Всё это синонимы. Напоминаю, что обратную матрицу 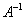 можно найти лишь для невырожденной квадратной матрицы можно найти лишь для невырожденной квадратной матрицы 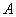 (определитель которой (определитель которой 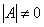 ), и со стандартным алгоритмом мы давно знакомы. Но есть и другой способ решения! ), и со стандартным алгоритмом мы давно знакомы. Но есть и другой способ решения!
Краткое содержание предстоящих действий таково: сначала следует записать квадратную матрицу 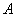 в тандеме с единичной матрицей: в тандеме с единичной матрицей: 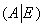 . Затем с помощью элементарных преобразований нужно получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом: . Затем с помощью элементарных преобразований нужно получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:
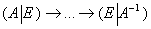 (понятно, что обратная матрица должна существовать). (понятно, что обратная матрица должна существовать).
Пример 125
Найти обратную матрицу с помощью элементарных преобразований
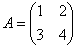
Решение: это матрица из Примера 58, где мы решили вопрос «обычным» методом. Но сейчас нам предписан другой путь. Запишем матрицу 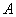 в одной упряжке с единичной матрицей, и применим алгоритм Гаусса-Йордана: в одной упряжке с единичной матрицей, и применим алгоритм Гаусса-Йордана:
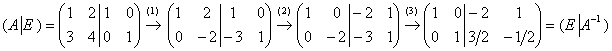
(1) Ко второй строке прибавили первую строку, умноженную на –3.
(2) К первой строке прибавили вторую строку.
(3) Вторую строку разделили на –2.
Ответ: 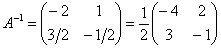
Но то была очередная «замануха» :) – обычно решение гораздо более длительно и кропотливо. Чаще всего предлагают матрицу «три на три»:
Пример 126
Найти обратную матрицу с помощью элементарных преобразований
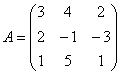
Решение: присоединяем единичную матрицу и начинаем выполнять преобразования, придерживаясь обычного алгоритма метода Гаусса:
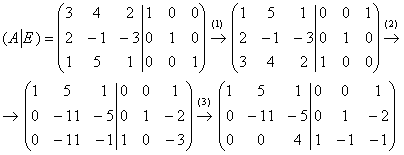
(1) Первую и третью строки поменяли местами (да, это можно делать и здесь).
(2) Ко второй строке прибавили первую, умноженную на –2. К третьей строке прибавили первую, умноженную на –3.
(3) К третьей строке прибавили вторую строку, умноженную на –1
Итак, матрица 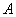 приведена к ступенчатому виду и полпути позади. Теперь в действие вступает алгоритм Гаусса-Йордана. Перестановка строк становится бессмысленной, но это нам не помешает аккуратно довести вычисления до конца, причём, без дробей. приведена к ступенчатому виду и полпути позади. Теперь в действие вступает алгоритм Гаусса-Йордана. Перестановка строк становится бессмысленной, но это нам не помешает аккуратно довести вычисления до конца, причём, без дробей.
Сначала нужно получить два нуля в третьем столбце. Для этого находим наименьшее общее кратное (НОК) чисел этого столбца (1, –5, 4): 20. Существует строгий алгоритм нахождения НОК, но здесь обычно хватает подбора. Ничего страшного, если взять бОльшее число, которое делится и на 1, и на –5, и на 4, например, 40. Отличие будет в более громоздких вычислениях. Используйте, кстати, калькулятор, тут это не зазорно.
Итак:
(4) Третью строку умножаем на 5, вторую строку на 4, первую строку на –20:
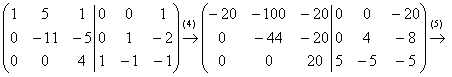
Цель такого домножения – получить одинаковые по модулю значения в третьем столбце, равные НОК, то есть 20 в данном случае. Зачем? Чтобы было проще выполнить следующее действие, избежав тем самым появление дробей:
(5) К первой строке прибавляем третью строку. Ко второй строке – её же, третью:
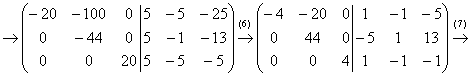
(6) Первую и третью строки разделили на 5, вторую строку умножили на –1.
И теперь нам нужно вымучить ещё один ноль – вверху второго столбца. Наименьшее общее кратное ненулевых чисел второго столбца (–20 и 44) равно 220.
(7) Чтобы получить во 2-м столбце одинаковые по модулю значения (равные 220), первую строку умножаем на 11, а вторую – на 5:
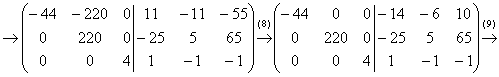
(8) К первой строке прибавили вторую строку и далее косметика.
(9) Первую строку умножаем на –1, вторую строку делим «обратно» на 5:
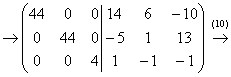
(10) Теперь на главной диагонали левой матрицы целесообразно получить наименьшее общее кратное чисел главной диагонали (44, 44 и 4). Совершенно понятно, что это число 44. А посему третью строку умножаем на 11
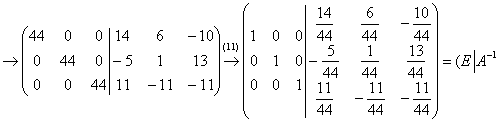
(11) Каждую строку делим на 44. И обратите внимание, что дроби у нас появились только на последнем шаге!
Таким образом, обратная матрица:
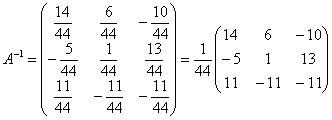 – записываем её в ответ. – записываем её в ответ.
Проверка выполняется стандартно.
Аналогичное задание для самостоятельного решения:
Пример 127
Найти обратную матрицу для 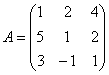 методом присоединенной матрицы методом присоединенной матрицы
Примерный образец оформления задачи в конце книги. Обязательно оценить красоту и, главное, удобство решения через НОК, по моему мнению, это самая надёжная схема решения. Продвинутый читатель может выполнить некоторые шаги устно, сократив тем самым запись, однако это чревато ПОВЫШЕННЫМ риском обсчитаться.
Иногда бывает удобно более короткое «модернистское» решение, которое заключается в следующем: на первом шаге всё как обычно:  . На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце: . На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце: 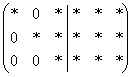 . Перед этим действием особенно трудно устоять, если во 2-м столбце нарисовались одинаковые по модулю числа, например, те же банальные «единицы». И, наконец, на третьем шаге точно так же (через НОК) получаем нужные нули в третьем столбце: . Перед этим действием особенно трудно устоять, если во 2-м столбце нарисовались одинаковые по модулю числа, например, те же банальные «единицы». И, наконец, на третьем шаге точно так же (через НОК) получаем нужные нули в третьем столбце: 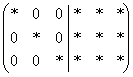 . Для любителей и любителей поневоле: . Для любителей и любителей поневоле:
Пример 128
Найти обратную матрицу для 
Это задание из моей собственной физматовской контрольной работы по алгебре, …эх, где мой первый курс? В 2001 году (листочек на удивление не пожелтел), я уложился в 8 шагов, а сейчас – всего лишь в 6! Решение – «модерн», но вы лучше используйте стандартные алгоритмы. …И тут, конечно, не нужно считать 17 определителей :)
 6. Векторные пространства и линейные преобразования 6. Векторные пространства и линейные преобразования
 5.10. Метод Гаусса-Йордана 5.10. Метод Гаусса-Йордана
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих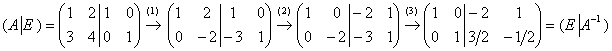
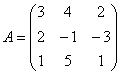
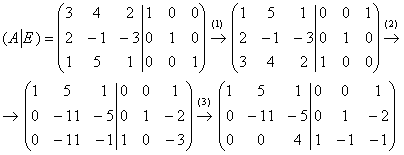
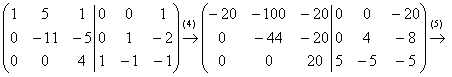
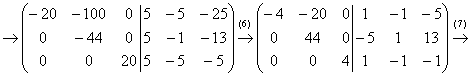
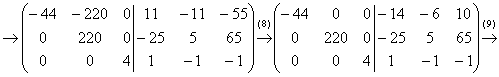
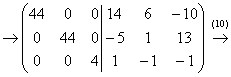

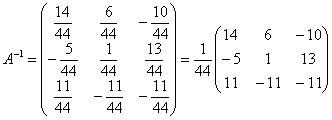 – записываем её в ответ.
– записываем её в ответ.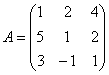 методом присоединенной матрицы
методом присоединенной матрицы . На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце:
. На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце:  . Перед этим действием особенно трудно устоять, если во 2-м столбце нарисовались одинаковые по модулю числа, например, те же банальные «единицы». И, наконец, на третьем шаге точно так же (через НОК) получаем нужные нули в третьем столбце:
. Перед этим действием особенно трудно устоять, если во 2-м столбце нарисовались одинаковые по модулю числа, например, те же банальные «единицы». И, наконец, на третьем шаге точно так же (через НОК) получаем нужные нули в третьем столбце:  . Для любителей и любителей поневоле:
. Для любителей и любителей поневоле:
 6. Векторные пространства и линейные преобразования
6. Векторные пространства и линейные преобразования 5.10. Метод Гаусса-Йордана
5.10. Метод Гаусса-Йордана