|
Ваш репетитор, справочник и друг!
|
5.5. Метод последовательного исключения неизвестных (Гаусса)Или метод Гаусса. На самом деле мы уже решали систему методом исключения неизвестных («школьный» метод), но сейчас в этом процессе появится закономерность и своя техника вычислений. А именно, нам понадобятся элементарные преобразования строк, поэтому если Вы по каким-то причинам пропустили этот параграф, то обязательно наверстайте упущенное! Вернёмся к системе Сначала нужно записать расширенную матрицу системы: По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления. Справка: рекомендую сразу запомнить термины. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: После того, как расширенная матрица системы записана, её нужно привести к ступенчатому виду. Как? С помощью элементарных преобразований строк. А почему это возможно? Элементарные преобразования не меняют множество решений системы! Чтобы привести матрицу Чистовое решение может выглядеть примерно так: запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду: При оформлении задачи от руки «лестницу» и «ступеньки» прямо так и отмечают простым карандашом: Итак, что же произошло? В результате элементарных преобразований мы перешли от исходной системы Теперь систему нужно «раскрутить» в обратном направлении, этот процесс называется обратным ходом метода Гаусса. В нижнем уравнении у нас уже готовый результат: Рассмотрим первое уравнение системы Ответ: Теперь разберём «классическое» задание, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными. Пример 104 Решить методом Гаусса систему уравнений: Решение: запишем расширенную матрицу системы: Сначала смотрим на левое верхнее число: Преобразование первое: меняем местами первую и третью строки: И первая строка у нас останется неизменной до конца решения. Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах: Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Для этого первую строку мысленно либо на черновике умножаем на «минус два»: (–2, –4, 2, –18) и ко 2-й строке прибавляем 1-ю, умноженную на –2 (смотрим и считаем снизу вверх): Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3. Мысленно или на черновике умножаем первую строку на «минус три»: (–3, –6, 3, –27), и На практике эти действия обычно выполняют последовательно (см. «пошаговый ход мыслей» выше), чаще всего устно, а результаты записывают в единую матрицу: Последнее выполненное действие – причёска результата, делим третью строку на 3. В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений: Круто. Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх. В третьем уравнении у нас готовый результат: Смотрим на второе уравнение: И, наконец, первое уравнение: Ответ: Не забываем выполнить устную либо письменную проверку! Пример 105 Решить систему линейных уравнений методом Гаусса Это пример для самостоятельного решения. Усложним задачу: Пример 106 Решить систему линейных уравнений методом Гаусса Решение: запишем расширенную матрицу системы Легко сказать…. Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица либо минус один. Но проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась: Заряжаем обратный ход. В оформлении примеров часто не пишут полученную эквивалентную систему, а уравнения «берут» прямо из приведённой (ступенчатой) матрицы. Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился: Выполняем устную проверку и записываем ответ: Следующая система для самостоятельного решения, она несколько сложнее. Пример 107 Решить систему линейных уравнений методом Гаусса Ничего страшного, если поплутаете немного :) Ваше решение может не совпасть с образцом, и это очевидная особенность метода Гаусса. Но вот ответы обязательно должны получиться одинаковыми! Ибо элементарные преобразования не меняют корни. Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если у вас внизу получилось что-нибудь вроде И в заключение параграфа рассмотрим некоторые особенности алгоритма. Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например: В этом случае в расширенной матрице системы на месте отсутствующих переменных ставим нули: Будьте ВНИМАТЕЛЬНЫ! Кстати, это довольно лёгкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований. Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? Конечно. Любые. Только вот в ходе вычислений нарисуются дроби (почти всегда), а оно вам надо? Однако в ряде случаев годятся и другие числа, рассмотрим, например, такую систему: Здесь на левой верхней «ступеньке» двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. Поэтому двойка нас устроит! И на первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце. Или другой условный пример: Иногда в системе могут изначально присутствовать дроби, даже десятичные: Метод Гаусса универсален, и работает для любой системы линейных уравнений, сколько в ней ни было переменных, уравнений, решений, и даже если решений вовсе нет. Но есть одна особенность… …Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, нужно «набить руку», и прорешать хотя бы 5-10 десять систем. Поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного. А посему сделаем ещё один шаг в правильном направлении: Пример 108 Решить систему методом последовательного исключения неизвестных Тренируемся, сверяемся с ответом и продолжаем. До сих пор мы рассматривали системы, которые имеют единственное решение. Такие системы можно решить любым способом: методом подстановки («школьным»), по формулам Крамера, матричным методом или только что разобранным методом Гаусса. Однако на практике встречаются ещё два случая: И для этих случаев срабатывают далеко не все методы решения. Кроме того, мы ведь заранее не знаем, сколько решений имеет та или иная система, и имеет ли их вообще. В этой связи по умолчанию (если в условии не сказано иного) стараются использовать наиболее универсальный – метод Гаусса.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих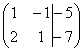
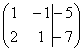 . Любую из матриц можно для краткости называть просто матрицей.
. Любую из матриц можно для краткости называть просто матрицей.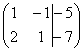 к ступенчатому виду, слева внизу нужно получить ноль. Для этого ко 2-й строке прибавим 1-ю, умноженную (МЫСЛЕННО либо на черновике) на –2. Напоминаю, что строка, которую мысленно умножают и прибавляют, остаётся неизменной, и если расписывать ход мыслей пошагово, то он таков:
к ступенчатому виду, слева внизу нужно получить ноль. Для этого ко 2-й строке прибавим 1-ю, умноженную (МЫСЛЕННО либо на черновике) на –2. Напоминаю, что строка, которую мысленно умножают и прибавляют, остаётся неизменной, и если расписывать ход мыслей пошагово, то он таков: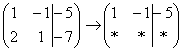 »
» 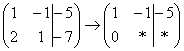 »
»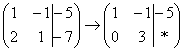 »
»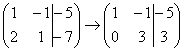 »
»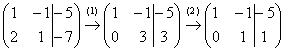
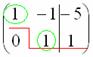
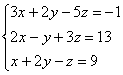
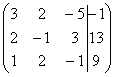
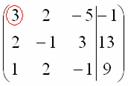
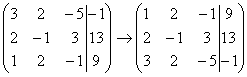
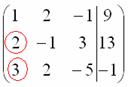
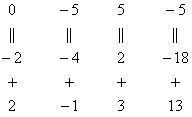
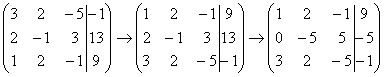
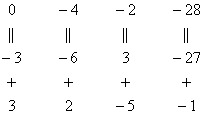
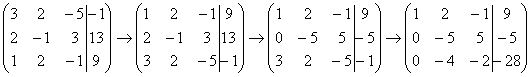
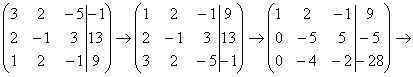
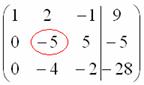
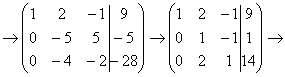
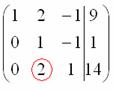
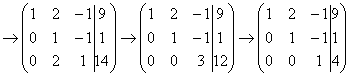
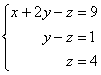
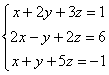
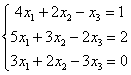
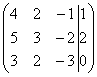 и с помощью элементарных преобразований приведём ее к ступенчатому виду.
и с помощью элементарных преобразований приведём ее к ступенчатому виду.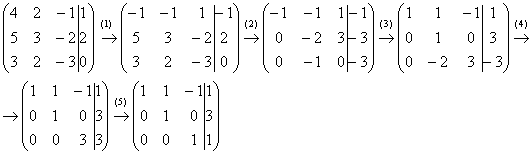
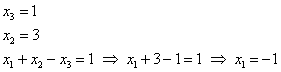
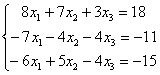
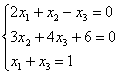
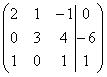
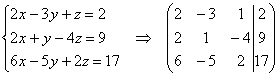
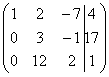 . Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Нужно провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.
. Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Нужно провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.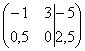
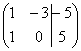
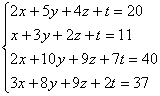
 5.6. Несовместные системы
5.6. Несовместные системы 5.4. Как решить систему с помощью обратной матрицы?
5.4. Как решить систему с помощью обратной матрицы?