|
Ваш репетитор, справочник и друг!
|
5.3. Метод КрамераКоторый также называют правилом Крамера или формулами Крамера. Начнём со скромной системы двух уравнений с двумя неизвестными: На первом шаге нужно вычислить главный определитель системы: Если Сразу улавливаем закономерность: столбец свободных членов подставляется в главный определитель сначала на 1-е место, затем на 2-е. Корни уравнения находим по формулам: Если главный определитель равен нулю Обозначения: помимо греческой буквы И возникает вопрос: зачем использовать правило Крамера? Ведь простейшую систему можно решить «школьным» методом, методом почленного сложения…. Ну, во-первых, такое задание реально встречается на практике – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Кроме того, этот способ встречается в учебной литературе, и он не должен вас застать врасплох. И, во-вторых, есть системы, которые удобно решить именно методом Крамера! Пример 96 Решить систему линейных уравнений Мы видим, что коэффициенты уравнений достаточно великИ, а в правой части присутствуют десятичные дроби. Запятая – довольно редкий гость в практических заданиях по математике, и этот пример я взял из эконометрической задачи. Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть плохо. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь появится страх. Что делать? В подобных случаях и приходят на помощь формулы Крамера. Решение: систему решим по правилу Крамера. Вычислим главный определитель: Внимание! Когда вы используете данный метод, обязательно прописывайте этот фрагмент: «
Ответ можно записать приближённо: И, конечно, проверка, которую удобно провести на калькуляторе: подставляем приближенные значения Пример 97 Решить систему по формулам Крамера. Ответ представить в обыкновенных неправильных дробях. Сделать проверку. Это пример для самостоятельного решения и ещё одна иллюстрация – если корни дробные, то удобен именно метод Крамера, который позволит избежать промежуточных дробных вычислений. А, кстати, когда может возникнуть такая ситуация? Если вы проводите какое-то теоретическое или практическое исследование и получили систему, то с высочайшей вероятностью её решение будет дробным. Тряхнём Пример 98 Решить систему уравнений, ответ представить в алгебраической и показательной форме, изобразить корни на чертеже. Решение: уже из условия можно предположить, что система имеет единственное решение, таким образом, нам нужно найти два числа Систему можно решить «детским» способом, однако гораздо лучше использовать формулы Крамера. По причине чёткости алгоритма и меньшей путаницы. Вычислим главный определитель системы: Не торопимся и прописываем шаги максимально подробно, ибо за комплексными числами нужен глаз да глаз: Домножаем числитель и знаменатель на мнимую единицу и получаем 1-й корень: Аналогично: Всё удачно сократилось, но, тем не менее, проверим решение. Подставим найденные значения
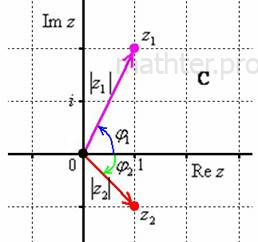
Выполним чертёж: Представим корни в показательной форме. Для этого нужно найти их модули и аргументы: 1) 2)
Ответ: Самостоятельно: Пример 99 Решить систему уравнений Запишем правило Крамера для системы трёх уравнений с тремя неизвестными: Главный определитель системы состоит из коэффициентов левых частей – строго в том порядке, в котором они находятся в
системе: Если Как видите, случай «три плюс три» принципиально ничем не отличается от случая «два плюс два», столбец свободных членов И ответ тоже рассчитывается по аналогичным формулам: С соточкой вас! Пример 100 Решить систему по формулам Крамера. Решение: вычислим главный определитель системы: Комментарии здесь не нужны, поскольку задание решается по готовым формулам, но вот затем будет о чём поговорить. Понеслось: Выполним (!) устную проверку и запишем ответ: Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например 1) Если под рукой есть компьютер или гаджет, то просто забиваем коэффициенты системы в Матричный калькулятор
(приложен к книге) и сверяемся. Как вариант, можно использовать онлайн калькулятор, к которому у Вас есть доверие. 2) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу проверьте, правильно ли переписано условие. Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу). 3) Если в результате проверки ошибок не выявлено, то либо допущена опечатка в условии, либо так оно и было задумано. В любом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовик. Да, проверка дробного ответа – занятие неприятное, но зато это будет обезоруживающий аргумент для рецензента, который ну очень любит ставить «–» за всякую бяку. И ещё одно замечание. Время от времени встречаются системы, в уравнениях которых в явном виде отсутствуют некоторые
переменные, например: Здесь в первом уравнении отсутствует переменная Ну и, конечно, не забываем о «золотом» правиле ;-) Пример 101 Решить систему по формулам Крамера. Это пример для самостоятельного решения. Для случая системы четырёх уравнений с четырьмя неизвестными формулы Крамера записываются по такому же принципу: главный определитель состоит из упорядоченных коэффициентов левой части, а во вспомогательных определителях столбец свободных членов последовательно «пробегает» слева направо. Такое задание встречается и вполне решабельно (понижением порядка определителя), хотя уже напоминает ботинок профессора на груди у студента-счастливчика.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих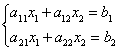
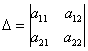 .
.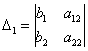 и
и 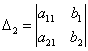

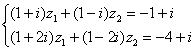
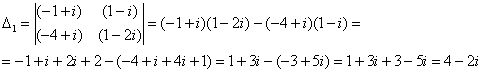
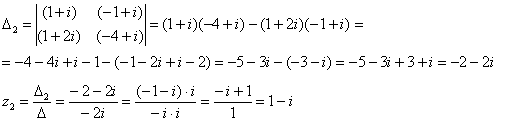
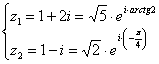
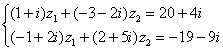 , выполнить проверку. Найти произведение
корней и записать результат в
, выполнить проверку. Найти произведение
корней и записать результат в 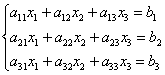
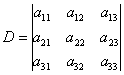
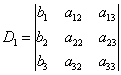 ,
, 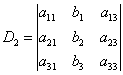 ,
, 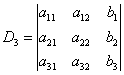
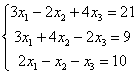
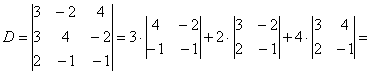



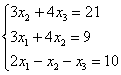
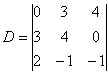 – на месте отсутствующих переменных ставятся
нули. По понятной причине, ведь недостающие слагаемые, они реальны:
– на месте отсутствующих переменных ставятся
нули. По понятной причине, ведь недостающие слагаемые, они реальны: 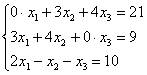 .
.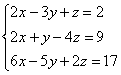
 5.4. Как решить систему с помощью обратной матрицы?
5.4. Как решить систему с помощью обратной матрицы? 5.2. Метод почленного сложения (вычитания) уравнений системы
5.2. Метод почленного сложения (вычитания) уравнений системы