|
Ваш репетитор, справочник и друг!
|
5.1. Решение системы линейных уравнений методом подстановкиЭтот метод также называют «школьным», «дедовским», «примитивным», чего я только не слышал за годы практики. Его суть состоит в том, чтобы выразить из какого-нибудь уравнения какую-нибудь переменную и подставить её в другие уравнения: Пример 90 Решить систему Здесь у нас дана система двух уравнений с двумя неизвестными. Свободные члены (числа 5 и 7) расположены слева и давайте перенесём их в
соответствующие правые части, чисто для удобства: Решаем: из первого уравнения выразим Раскрываем скобки, приводим подобные слагаемые и находим значение Теперь вспоминаем про то, от чего плясали: Значение После того, как решена ЛЮБАЯ система уравнений ЛЮБЫМ способом, настоятельно рекомендую выполнять проверку: устно, на черновике или калькуляторе. Благо, делается это легко и быстро: 1) Подставим найденный набор 2) Подставляем найденный набор Таким образом, значения Ответ: Рассмотренный способ решения не является единственным, из первого уравнения можно было выразить Можно наоборот – что-нибудь выразить из второго уравнения Получаются дроби, а оно зачем? Есть более рациональные пути. Но, очевидно, в ряде случаев без дробей не обойтись, ибо системы бывают разные. И на всякий пожарный повторю мантру: в высшей математике все действия стремимся проводить в обыкновенных (правильных и неправильных) дробях. А посему пишем Итак, если вам встретилась система двух линейных уравнений с двумя неизвестными, то всегда можно использовать метод подстановки (если не указано, что систему нужно решить другим способом) Ни один преподаватель не подумает, что ты лох снизит оценку за использование «школьного» метода. Особенно, если это какие-то промежуточные вычисления в рамках другого задания. Более того, в ряде случаев метод подстановки целесообразно использовать и при бОльшем количестве переменных: Пример 91 Решить систему линейных уравнений с тремя неизвестными Такая система с такими буквами возникает в ходе решения некоторых интегралов и дифференциальных уравнений, где наша цель – БЫСТРО найти
значения Решение: когда нам дана любая система уравнений, в первую очередь желательно посмотреть, а нельзя ли её как-нибудь СРАЗУ упростить? Анализируя уравнения системы, замечаем, что второе уравнение можно разделить на 2, что мы и делаем: Теперь нужно выразить какую-нибудь переменную через остальные. Какое уравнение выбрать? Наверное, Вы уже догадались, что проще всего для
этой цели взять первое уравнение системы и выразить из него, например, «цэ» (так же удобно «а» либо «бэ»): Проверка: подставим найденные значения В результате получены соответствующие правые части уравнений или, как говорят в народе, «всё сошлось». Ответ: Следующая система для самостоятельного решения: Пример 92
Ваше решение, естественно, может отличаться от моего.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих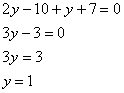
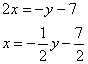
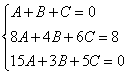
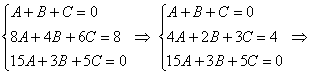
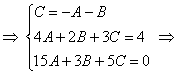
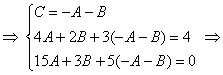
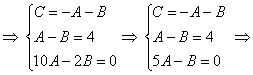
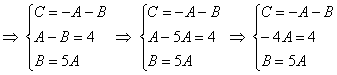
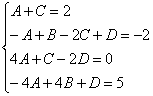
 5.2. Метод почленного сложения (вычитания) уравнений системы
5.2. Метод почленного сложения (вычитания) уравнений системы 5. Системы линейных алгебраических уравнений
5. Системы линейных алгебраических уравнений