5. Системы линейных алгебраических уравнений
Алгебраическое уравнение первой степени – это многочленное уравнение вида 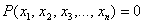 с «эн» неизвестными. И определение боксёра: система линейных алгебраических уравнений (СЛАУ, далее просто СЛУ) – это система, состоящая из линейных алгебраических уравнений, запишу её в общем виде: с «эн» неизвестными. И определение боксёра: система линейных алгебраических уравнений (СЛАУ, далее просто СЛУ) – это система, состоящая из линейных алгебраических уравнений, запишу её в общем виде:
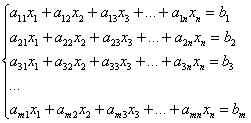
Перед вами система «эм» линейных уравнений с «эн» неизвестными 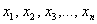 , где , где 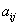 (все помнят смысл подстрочных индексов?) – числа, чаще всего действительные, и (все помнят смысл подстрочных индексов?) – числа, чаще всего действительные, и  – тоже числа, которые называют свободными членами. – тоже числа, которые называют свободными членами.
Неизвестные, помимо версии 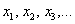 , также обозначают , также обозначают 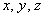 («школьный» вариант), маленькими («школьный» вариант), маленькими 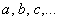 либо большими либо большими 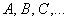 буквами латинского алфавита. Не так уж редко можно встретить греческие буквы: буквами латинского алфавита. Не так уж редко можно встретить греческие буквы: 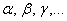 – пресловутые «альфа, бета, гамма», в том числе с подстрочными индексами: – пресловутые «альфа, бета, гамма», в том числе с подстрочными индексами: 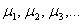 («мю первое» и т. д.). Использование того или иного набора букв зависит от раздела математики, в котором мы сталкиваемся с системой. («мю первое» и т. д.). Использование того или иного набора букв зависит от раздела математики, в котором мы сталкиваемся с системой.
Решить систему линейных уравнений – это значит найти множество значений 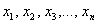 , которые удовлетворяют КАЖДОМУ уравнению системы (обращают их в верные числовые равенства) либо доказать, что решений нет. , которые удовлетворяют КАЖДОМУ уравнению системы (обращают их в верные числовые равенства) либо доказать, что решений нет.
Система может (одно из трёх):
1) иметь единственное решение 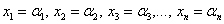 , ,
2) иметь бесконечно много решений (бесконечное количество наборов значений 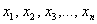 ), ),
3) не иметь решений (быть несовместной). Существует несколько способов решения системы, и начнём мы с повторения:
 5.1. Решение системы линейных уравнений методом подстановки 5.1. Решение системы линейных уравнений методом подстановки
 4.14.6. Как найти ранг матрицы с помощью элементарных преобразований? 4.14.6. Как найти ранг матрицы с помощью элементарных преобразований?
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих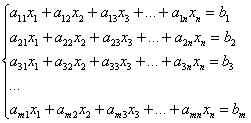
 5.1. Решение системы линейных уравнений методом подстановки
5.1. Решение системы линейных уравнений методом подстановки 4.14.6. Как найти ранг матрицы с помощью элементарных преобразований?
4.14.6. Как найти ранг матрицы с помощью элементарных преобразований?