|
Ваш репетитор, справочник и друг!
|
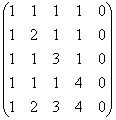
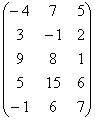
4.14.6. Как найти ранг матрицы с помощью элементарных преобразований?Для этого нужно привести матрицу к ступенчатому виду. Сначала поймём, что такое ступенчатый вид на интуитивном уровне: Как видите, высота всех «ступенек» строго одинакова. Но можно дать формальное определение. Любая матрица-строка считается ступенчатой, «замазали» этот частный случай. Первый ненулевой элемент строки (если смотреть слева направо) назовём ведущим. Матрица имеет ступенчатый вид, если ведущий элемент каждой последующей строки расположен строго правее ведущего элемента предыдущей строки. Нулевые строки договоримся удалять (хотя теоретически их можно расположить внизу). А вот примеры матриц, которые не имеют ступенчатого вида: В первой матрице ведущий элемент 2-й строки расположен левее ведущего элемента 1-й строки (а должен правее). Во второй матрице ведущий элемент 3-й строки расположен под ведущим элементом 2-й строки (а должен строго правее). И в третьей матрице аналогичная, ещё более грубая история в 4-й строке. Но это не беда. Ведь матрицы можно привести к ступенчатому виду. Так, в первом случае достаточно переставить строки: Во второй матрице к 3-й строке прибавим 2-ю, умноженную (мысленно или на черновике) на –2: И в третьей матрице к 4-й строке прибавим 1-ю, умноженную (мысленно) на –1: Ранг ступенчатой матрицы равен количеству её ненулевых строк. И поскольку элементарные преобразования не меняют ранг матрицы, то алгоритм предельно прост: 1) с помощью элементарных преобразований приводим исходную матрицу (если это не строка) к ступенчатому виду; 2) ранг исходной матрицы равен количеству ненулевых строк ступенчатой матрицы. Вернёмся к матрице «три на три» с координатами трёх коллинеарных векторов. Поскольку строки матрицы пропорциональны, то нужно оставить только одну из них: Ранг ступенчатой матрицы равен одному (т. к. это ненулевая строка), и поэтому ранг исходной матрицы тоже единица. Что и говорить, это гораздо быстрее, чем рассчитать девять нулевых миноров 2-го порядка и только потом сделать вывод о том, что Но на практике линейную зависимость строк можно не заметить, и, кроме того, она бывает вовсе не очевидной. Никаких проблем – просто начинаем приводить матрицу к ступенчатому виду. Слева вверху обычно располагают единицу либо «минус» единицу (иначе появятся дроби, скорее всего), и нам нужно получить нули вот на этих местах: Для этого ко 2-й строке прибавим 1-ю строку, умноженную (мысленно или на черновике) на –2. Ну а к 3-й строке просто прибавляется 1-я (без всяких домножений): Рассмотрим более содержательный пример: Пример 85 Найти ранг матрицы с помощью элементарных преобразований Решение: здесь сразу бросается в глаза, что 3-ю строку можно разделить на 5, и мы это делаем, чтобы упростить вычисления. Слева вверху нужно организовать единицу, для этого на втором шаге меняем 1-ю и 3-ю строки местами: Теперь в первом столбце нужно получить нули под единицей. Для этого ко 2-й строке прибавим 1-ю, умноженную (мысленно или на черновике) на –1. И к 3-й строке тоже прибавим 1-ю, только умноженную уже на –2: Внимание ещё раз! При выполнении этого преобразования вновь возникает соблазн вычесть из 2-й строки 1-ю (и записать результат во вторую). Да, это тоже правильно, но старайтесь так не делать, вычитание повышает риск ошибки. Только складываем! Далее работаем со 2-й и 3-й строкой. На второй «ступеньке» (в качестве ведущего элемента 2-й строки) снова нужно получить единицу. И тут в общем случае могут быть варианты. Если бы внизу вместо тройки была единица, то вопрос решён – просто переставляем 2-ю и 3-ю строки местами. Но у нас другая ситуация, и единицу придётся организовать с помощью дополнительного преобразования. Ко 2-й строке прибавим 3-ю строку, умноженную (мысленно или на черновике) на –1: В ступенчатой матрице три строки (здесь и далее подразумеваем – ненулевые), поэтому её ранг, а значит, и ранг исходной матрицы равен трём. Ответ: Увеличим размеры: Пример 86 Найти ранг матрицы с помощью элементарных преобразований Решение: сначала нужно организовать 1 либо –1 слева вверху. Но в первом столбце единиц нет, и поэтому перестановка строк не поможет. Как быть? Кол можно получить с помощью элементарного преобразования (например, к 1-й строке прибавить 4-ю, умноженную на –1). Но зачем лишние действия? Ведь переставлять можно и столбцы! Тут даже выбор есть. Несколько выгоднее использовать 2-й столбец, так как в нём числа получше. Итак, на первом шаге (1) меняем местами 1-й и 2-й столбец: (2) Теперь ниже нашего «колА» нужно получить нули в первом столбце. Ко 2-й строке прибавляем 1-ю строку, умноженную на –1. Не вычитаем! То же самое проделываем с 3-й строкой. И к 4-й строке прибавляем 1-ю строку, умноженную на –2. (3) Последние три строки пропорциональны, оставляем одну из них. Ступенчатая матрица получена и состоит из двух строк, поэтому её ранг, а значит, и ранг исходной матрицы равен двум. Ответ: Теперь ваша очередь мучить матрицу: Пример 87 Найти ранг матрицы с помощью элементарных преобразований: Ваше решение может отличаться от образца, так как алгоритм не однозначен. Есть разные пути с разными элементарными преобразованиями. На практике часто не сказано, какой метод нужно использовать для нахождения ранга. В такой ситуации следует анализировать условие – для небольших матриц хорошо смотрится прямой перебор миноров либо метод окаймляющих миноров. Но если размеры приличны, то, конечно, элементарные преобразования: Пример 88 Найти ранг матрицы Решение с помощью миноров как-то сразу отпадает =) Сначала преобразования, затем комментарии: (1) Пятый столбец нулевой, удаляем его из матрицы. И здесь я познакомлю вас с ещё одной фирменной «фишкой» алгоритма: первую строку умножаем на –1. …Зачем? Чтобы превратить следующий пункт в халяву. (2) Ко всем строкам, начиная со второй, прибавляем первую строку. (3) Первую строку умножаем на –1 (убираем теперь ненужные минусы), третью строку делим на 2, четвёртую строку делим на 3. К пятой строке прибавляем вторую строку, умноженную на –1. (4) К пятой строке прибавляем третью строку, умноженную на –2. (5) Последние две строки пропорциональны, оставляем одну из них. Полученная матрица имеет ступенчатый вид и содержит 4 строки, поэтому её ранг, а значит, и ранг исходной матрицы равен четырём. Ответ: Пятиэтажка для самостоятельного исследования: Пример 89 Найти ранг матрицы Краткое решение и ответ в конце книги.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих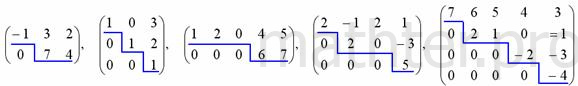
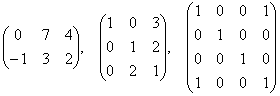
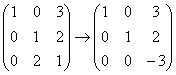 – получая на нужном месте ноль и ступенчатый вид.
– получая на нужном месте ноль и ступенчатый вид.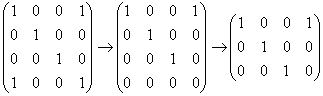
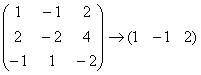
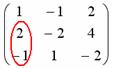
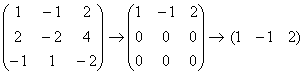

 , как вариант, можно было поменять местами 1-ю и 2-ю строки, но во второй числа больше, и это менее выгодный путь.
, как вариант, можно было поменять местами 1-ю и 2-ю строки, но во второй числа больше, и это менее выгодный путь.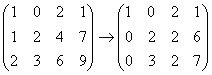
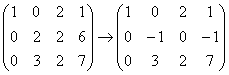
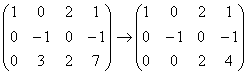 , ещё здесь можно умножить 2-ю строку на –1 и 3-ю строку разделить на 2, но в данной ситуации это уже ненужная косметика. Ибо ступенчатый вид получен.
, ещё здесь можно умножить 2-ю строку на –1 и 3-ю строку разделить на 2, но в данной ситуации это уже ненужная косметика. Ибо ступенчатый вид получен.
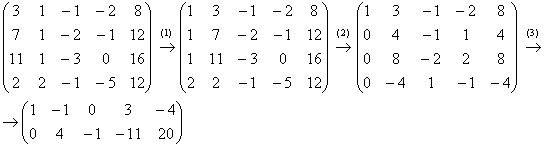
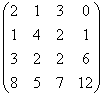

 5. Системы линейных алгебраических уравнений
5. Системы линейных алгебраических уравнений 4.14.5. Элементарные преобразования матрицы
4.14.5. Элементарные преобразования матрицы