|
Ваш репетитор, справочник и друг!
|
4.14.4. Метод окаймляющих миноровАлгоритм в общем виде, боюсь, будет мало кому понятен, поэтому разберём его в конкретной задаче: Пример 83 Найти ранг матрицы методом окаймляющих миноров Решение: дана квадратная матрицы «четыре на четыре» и совершенно понятно, что её ранг не превосходит четырёх. Так как в матрице есть ненулевые элементы, то её ранг не меньше единицы. Проверку миноров 2-го порядка начинаем с так называемого углового минора, Что было бы нужно сделать, если бы и этот минор оказался нулевым? В этом случае рассматриваем минор: Если же все миноры 2-го порядка оказались нулевыми, то Но в нашем случае «хороший» минор встретился уже во второй попытке, и теперь мы переходим к рассмотрению миноров третьего порядка. Приделываем ноги малышу Начнём с красного: Миноров 3-го порядка на самом деле больше, и рассматриваемый метод в данном случае позволяет сократить вычисления, максимум, до четырёх определителей. Успех нас поджидал в третьей попытке, и ненулевой минор Теперь «синие» и «малиновые» столбцы должны входить во все миноры высших порядков. В данном случае это единственный минор 4-го порядка, совпадающий с определителем матрицы: Если бы Ответ: максимальный порядок ненулевого минора равен трём, значит, …Возможно, не все до конца осмыслили данную фразу: минор 4-го порядка равен нулю, но среди миноров 3-го порядка нашёлся ненулевой – поэтому максимальный порядок ненулевого минора и равен трём. Возникает вопрос, а почему бы сразу не вычислить определитель? Ну, во-первых, в большинстве заданий матрица не квадратная, а во-вторых, даже если и получится ненулевое значение, то задание, скорее всего, будет забраковано, поскольку подразумевает стандартное решение «снизу вверх». А в рассмотренном примере нулевой определитель 4-го порядка и вовсе позволяет утверждать лишь то, что ранг матрицы меньше четырёх. Самостоятельно: Пример 84 Найти ранг матрицы методом окаймляющих миноров Решение с краткими комментариями в конец книги Когда алгоритм работает быстрее всего? Вернёмся к той же матрице «четыре на четыре»: Размышление совсем не гипотетично – встречается немало примеров, где всё дело и ограничивается только угловыми минорами. Однако в ряде случаев более эффективен и предпочтителен другой способ нахождения ранга, но сначала подготовимся к нему:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих
 .
.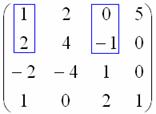

 ,
,  ,
,  .
.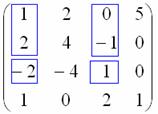
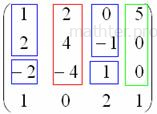
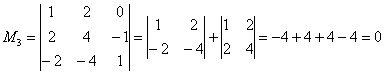
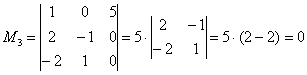
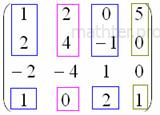
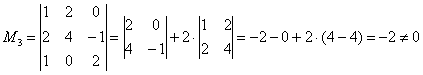 , значит, ранг матрицы не меньше трёх. Если бы этот минор оказался равным нулю, то следовало бы вычислить определитель из «синих» и «коричневых» чисел. Других миноров 3-го порядка, которые содержат младший ненулевой минор
, значит, ранг матрицы не меньше трёх. Если бы этот минор оказался равным нулю, то следовало бы вычислить определитель из «синих» и «коричневых» чисел. Других миноров 3-го порядка, которые содержат младший ненулевой минор 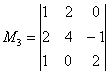 удостаивается ботинок:
удостаивается ботинок: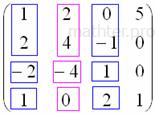
 (так как 2-я и 3-я строки пропорциональны)
(так как 2-я и 3-я строки пропорциональны)
 . Очевидно, решение будет самым коротким в случае «хороших» угловых миноров:
. Очевидно, решение будет самым коротким в случае «хороших» угловых миноров: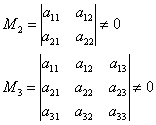
 4.14.5. Элементарные преобразования матрицы
4.14.5. Элементарные преобразования матрицы 4.14.3. Как найти ранг матрицы с помощью миноров?
4.14.3. Как найти ранг матрицы с помощью миноров?