|
Ваш репетитор, справочник и друг!
|
4.14.3. Как найти ранг матрицы с помощью миноров?В качестве примера возьмём ту же матрицу Поскольку в матрице есть ненулевые элементы, то её ранг не меньше единицы и, очевидно, что он не превосходит четырёх. Как действовать дальше? Дальше начинаем перебор и вычисление миноров 2-го порядка. Если ВСЕ миноры 2-го порядка окажутся нулевыми, то ранг матрицы равен единице. Но это крайне маловероятно, рано или поздно (чаще всего рано), встретится ненулевой минор На следующем шаге последовательно перебираем и рассчитываем миноры 3-го порядка. Если ВСЕ эти миноры равны нулю, то Перебор и вычисление миноров 4-го порядка. Если ВСЕ миноры 4-го порядка равны нулю, то Таким образом, ранг матрицы равен максимальному порядку ненулевого минора. Схему «перебора в лоб» можно раскритиковать, но как ни странно, во многих случаях она даёт неплохие результаты. Тем не менее, следует отметить возможную длительность процесса и в целях сокращения перебора разработан:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих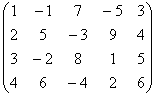 и рассмотрим алгоритм нахождения
и рассмотрим алгоритм нахождения  4.14.4. Метод окаймляющих миноров
4.14.4. Метод окаймляющих миноров 4.14.2. Миноры прямоугольной матрицы (общее определение)
4.14.2. Миноры прямоугольной матрицы (общее определение)