|
Ваш репетитор, справочник и друг!
|
4.14. Ранг матрицыПриветствую вас в «чемпионском» параграфе! 4.14.1. Что такое ранг матрицы?Само слово «ранг» у нас обычно ассоциируется с некоторой иерархией, чаще всего, со служебной лестницей. Чем больше у человека знаний, опыта, способностей, «блата» и т. д. – тем выше его статус и спектр возможностей. Выражаясь по молодёжному, под рангом подразумевают общую степень «крутизны». И братья наши математические живут по тем же принципам. Рассмотрим несколько произвольных нулевых матриц: Задумаемся, если в матрице одни нули, то о каком ранге может идти речь? Всем знакомо неформальное выражение «полный ноль». В обществе матриц всё точно так же. Ранг нулевой матрицы Далее для лучшего понимания я буду привлекать на помощь аналитическую геометрию, особо рекомендую уроки о линейной (не)зависимости векторов и базисе. Ознакомьтесь хотя бы бегло (если ещё не успели), будет намного легче! Рассмотрим нулевой вектор Теперь рассмотрим несколько ненулевых столбцов и строк: Ранг любой ненулевой строки или столбца равен единице. И вообще, если в любой матрице есть хотя бы один ненулевой элемент, то её ранг не меньше единицы. И вновь обратимся к геометрической ассоциации. Ненулевой вектор Рассмотрим матрицу Перепишем координаты векторов в столбцы (транспонируем матрицу): Что изменилось с точки зрения ранга? Ничего. Столбцы пропорциональны, значит, ранг равен единице. Кстати, обратите внимание, что все три строки тоже пропорциональны. Их можно отождествить с координатами трёх коллинеарных векторов плоскости, из которых только один полезен для построения «плоского» базиса. И это полностью согласуется с нашим геометрическим смыслом ранга. Из вышеприведённого примера следует важная гипотеза: Ранг матрицы по строкам равен рангу матрицы по столбцам. И это правда! Впрочем, с равноправием строк и столбцов мы уже столкнулись в ходе изучения свойств определителя. Таким образом, из линейной зависимости строк, следует линейная зависимость столбцов. То же касается и независимости. Однако в целях экономии времени, да и в силу привычки, я почти всегда буду говорить о линейной зависимости строк. Продолжим вскармливать нашего питомца. Добавим в матрицу третьей строкой координаты ещё одного коллинеарного вектора Продвинуло ли это нас в построении трёхмерного базиса? Конечно, нет. Все три вектора гуляют туда-сюда по одному направлению, поэтому ранг матрицы равен единице. Можно взять сколько угодно коллинеарных векторов, скажем, 100, уложить их координаты в матрицу «сто на три» и ранг такого небоскрёба всё равно останется единичным. Теперь смотрим на матрицу А чему равен ранг матрицы Как видите, линейная зависимость в этой матрице не очевидна, и сегодня мы как раз научимся выводить её «на чистую воду».…Думаю, многие уже прочувствовали, что такое ранг матрицы! И, наконец, в строки матрицы Как вы знаете, любой четвёртый, пятый, десятый вектор трёхмерного пространства будет линейно выражаться через базисные векторы. Поэтому, если в эту матрицу добавить любое количество строк, то её ранг всё равно будет равен трём. Аналогичные рассуждения можно провести для матриц бОльших размеров (понятно, уже без геометрического смысла). Ранг матрицы – это максимальное количество линейно независимых строк. И эквивалентное определение: ранг матрицы – это максимальное количество линейно независимых столбцов. Из вышесказанного следует важный практический ориентир: ранг матрицы не превосходит её минимальной размерности. Так, например, в матрице Обозначения: в мировой теории и практике не существует общепринятого стандарта для обозначения ранга матрицы:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих
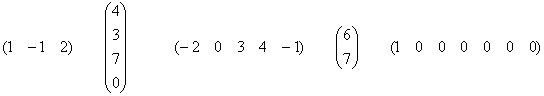
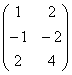
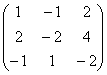
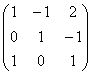 ? Строки вроде не пропорциональны…, значит, по идее трём. Однако ранг этой матрицы тоже равен двум. Я сложил первые две строки и записал результат внизу, то есть линейно выразил третью строку через первые две. Геометрически строки матрицы соответствуют координатам трёх компланарных векторов, но среди этой тройки есть пара неколлинеарных друзей. Ранг матрицы равен двум.
? Строки вроде не пропорциональны…, значит, по идее трём. Однако ранг этой матрицы тоже равен двум. Я сложил первые две строки и записал результат внизу, то есть линейно выразил третью строку через первые две. Геометрически строки матрицы соответствуют координатам трёх компланарных векторов, но среди этой тройки есть пара неколлинеарных друзей. Ранг матрицы равен двум.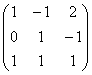 я записал координаты некомпланарных (линейно независимых) векторов
я записал координаты некомпланарных (линейно независимых) векторов 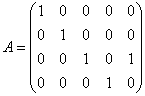 четыре строки и пять столбцов. Минимальная размерность – четыре, следовательно, ранг данной матрицы заведомо не превзойдёт четырёх. Кстати, тут очень хорошо видно, чему равен ранг ;)
четыре строки и пять столбцов. Минимальная размерность – четыре, следовательно, ранг данной матрицы заведомо не превзойдёт четырёх. Кстати, тут очень хорошо видно, чему равен ранг ;) 4.14.2. Миноры прямоугольной матрицы (общее определение)
4.14.2. Миноры прямоугольной матрицы (общее определение) 4.13. Матричные уравнения
4.13. Матричные уравнения