|
Ваш репетитор, справочник и друг!
|
4.13. Матричные уравненияНачнём с детского уравнения, например, Выполним проверку – подставим найденное значение Матричные уравнения устроены практически так же, только состоят они… правильно – из матриц (и конечно, числа тоже встречаются, помним, что матрицу можно умножить на число). Плюс особенные фишки, характерные для действий с матрицами. Всё просто, и особых трудностей возникнуть не должно. Типовое матричное уравнение состоит, как правило, из нескольких матриц и неизвестной матрицы Пример 77 Решить матричное уравнение, выполнить проверку Как решить матричное уравнение? Фактически нужно использовать алгоритм решения «школьного» уравнения. В правой части умножаем каждый элемент матрицы на три, а матрицу левой части переносим направо со сменой знака: Выполним вычитание в правой части: Все числа матрицы делятся на 2, поэтому уместно избавиться от дроби. А заодно и от «минуса». Делим каждый элемент матрицы на –2 и получаем Как выполнить проверку? Подставим найденное значение Всегда ли матричное уравнение имеет решение? Конечно не всегда. С ходу привожу простейшее доказательство, точнее, показательствоJ: Пример, который мы прорешали, элементарен, а посему перейдём к более содержательным заданиям, которые с большой вероятностью и встретятся вам на практике. Но прежде систематизируем общий ход решения. Алгоритм решения типового матричного уравнения На первом шаге уравнение приводится к одному из трёх видов: Как привести уравнение к одному из этих видов? Все действия вы только что видели – это перенос матриц из части в часть со сменой знака, внесение множителей в матрицы, матричное сложение / вычитание. На втором шаге нужно выразить 1) * ! Произведение матриц не перестановочно, поэтому критически важно, с какой стороны проводить умножение. Как мы знаем, Чего и требовалось достичь. Обращаю внимание, что матрица 2) «Зеркальная» ситуация: И ввиду того, что Готово. Матрица 3) И более редкий случай На третьем шаге находим обратную матрицу На заключительном четвёртом шаге выполняем матричное умножение После выполнения задания желательно провести проверку, впрочем, в большинстве случаев она требуется по условию. Схема обыденна – нужно подставить найденную матрицу Пример 78 Решить матричное уравнение, выполнить проверку Решение: предложенное уравнение имеет готовый вид Да-да, прямо так и пишем при оформлении решения. Хотя, в принципе, можно ограничиться единственной фразой: «Решение ищем в виде Матрицы Таким образом, обратная матрица: На финише проводим матричное умножение и получаем корень: Проверка: подставим найденное значение Ответ: Повысим ставки: Пример 79 Решить матричное уравнение и сделать проверку: Решение: неизвестная Для разрешения уравнения относительно Обратную матрицу найдем по формуле Обратная матрица: Таким образом, получаем: Проверка: подставим найденное значение Ответ: Дробь лучше не вносить в столбец. Получится некрасиво. Самостоятельно: Пример 80 Решить матричное уравнение, выполнить проверку Примерный чистовой образец оформления задачи в конце книги. Теперь отработаем второй тип уравнения. Алгоритм решения точно такой же, с некоторыми содержательными и техническими отличиями: Пример 81 Решить матричное уравнение, сделать проверку Решение: незнакомец расположился слева от матрицы, поэтому уравнение сведётся к виду Для разрешения уравнения относительно Обратную матрицу найдем по формуле Таким образом, обратная матрица: В результате получаем: …Геморрой, конечно, но ещё не тот, в целях проверки подставим найденное значение Ответ: Следующее задание для самостоятельного решения: Пример 82 Решить матричное уравнение и сделать проверку: Краткое решение и ответ в конце книги. И в заключение параграфа кратко остановлюсь на 3-м типе матричного уравнения: Да, работёнки здесь будет побольше. Раза в два. Как решить данное уравнение? – для матрицы Желающие могут прорешать это уравнение, верный ответ:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих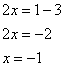
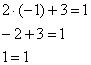
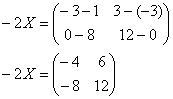
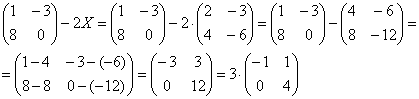
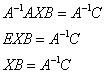
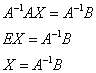
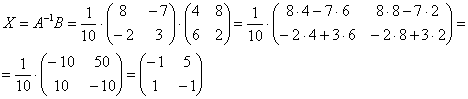
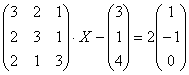
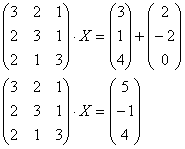
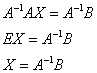
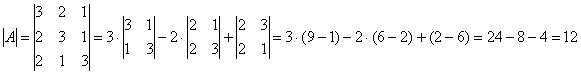
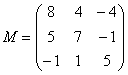 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы 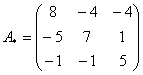 – матрица алгебраических дополнений.
– матрица алгебраических дополнений.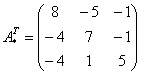 – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.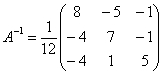
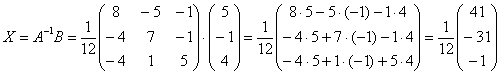
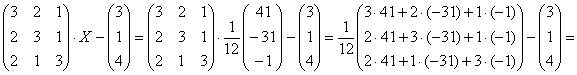
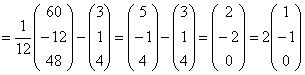 – получена правая часть исходного уравнения, и мы счастливы. Заметьте, что после подстановки
– получена правая часть исходного уравнения, и мы счастливы. Заметьте, что после подстановки 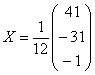
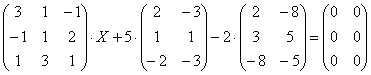
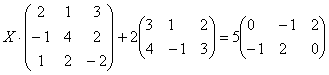
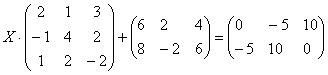
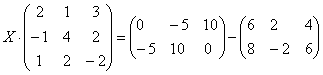
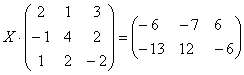
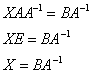
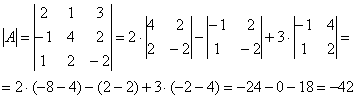
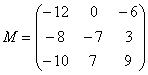 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы 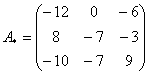 – матрица алгебраических дополнений.
– матрица алгебраических дополнений.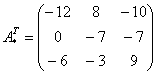 – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.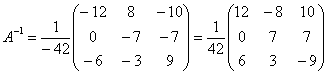
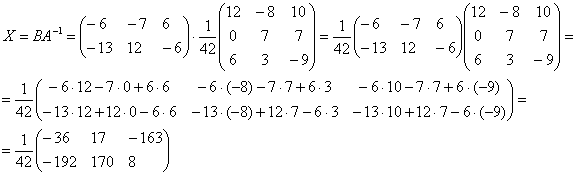
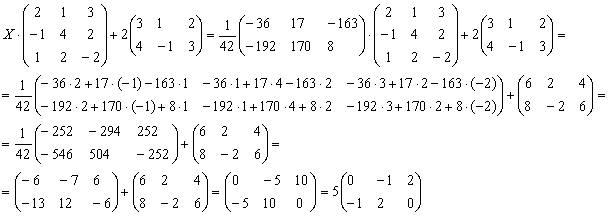
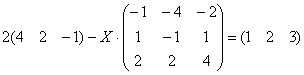
 4.14. Ранг матрицы
4.14. Ранг матрицы 4.12. Понижение порядка определителя
4.12. Понижение порядка определителя