|
Ваш репетитор, справочник и друг!
|
4.6. Миноры и алгебраические дополненияТолько что мы освоили упрощенный алгоритм расчёта определителей, но пришло время познакомить вас с более строгими обозначениями и терминологией. Заодно дадим определение определителя. Начнём с компактного обозначения матрицы: Эта запись обозначает матрицу, состоящую из элементов Смысл двойных подстрочных индексов: первое число обозначает номер строки, в котором расположен элемент, а второе число
– номер столбца: Это СТАНДАРТ. И не только в алгебре. Запомните данный факт! Рассмотрим скромную матрицу Подстрочные индексы элемента Хорошо, едем дальше. Минором элемента Алгебраическим дополнением элемента Так, в матрице «два на два» минором элемента Минор элемента Определитель матрицы – это сумма произведений элементов любой строки либо столбца на соответствующие алгебраические дополнения. Разложим определитель матрицы «два на два», например, по 1-му столбцу: Самостоятельно разложИте этот определитель тремя другими способами и убедитесь, что получится то же самое. Теперь наиболее популярный случай: Найдём определитель этой матрицы, например, по первой строке. По определению: …Знакомая картинка, не правда ли? По существу, в «матрице знаков» я замаскировал алгебраические дополнения, дабы не утопить начинающих в терминах. Ну а с маленькими определителями «два на два» снова разбираемся по определению определителя (см. выше), в результате чего получится не что иное, как формула треугольников. И смотрИте, какАя штука: приведённое выше определение определителя определяет его через алгебраические дополнения, то есть, по сути, через другие определители (миноры). Такую схему называют рекурсией. И, используя рекурсивное определение определителя, можно получить формулу для вычисления определителя любого порядка. Следует сказать, что определение определителя чаще всего даётся через так называемые перестановки и инверсии (из чего, кстати, следует только что упомянутая формула) Но это достаточно громоздкие выкладки, которые я оставлю за рамками настоящей книги, а то здесь нарисуется ещё две страницы крякозябр :D, и «чайники» таки утонут.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих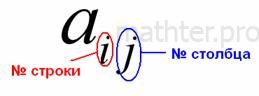

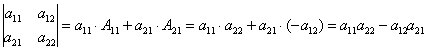 , в результате чего получена известная нам
формула.
, в результате чего получена известная нам
формула.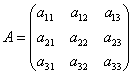 ! Проговорите вслух, что означают
подстрочные индексы!
! Проговорите вслух, что означают
подстрочные индексы! 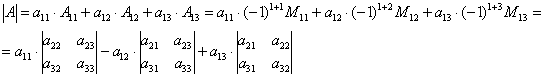
 4.7. Обратная матрица
4.7. Обратная матрица 4.5.4. Раскрытие определителя по строке или по столбцу
4.5.4. Раскрытие определителя по строке или по столбцу