|
Ваш репетитор, справочник и друг!
|
4.12. Понижение порядка определителяОбъяснять сразу буду на конкретном примере: Пример 73 Вычислить определитель, понизив его порядок Суть задания состоит в том, искусственно получить два нуля в какой-нибудь строке (или столбце) и свести решение к вычислению определителя «два на два». Нули получают с помощью так называемых элементарных преобразований, с одним из которых мы познакомимся прямо сейчас. С чего начать? Сначала в определителе нужно выбрать число-«мишень». В качестве «мишени» почти всегда выступает единица либо «минус единица». Смотрим на определитель и замечаем, что здесь даже выбор есть. Пусть числом-«мишенью» будет элемент Напоминаю смысл двойных подстрочных индексов: индексы элемента Теперь нам нужно получить два нуля в третьем столбце (на красных местах): 1) Путь первый. Организуем нули в третьем столбце: Правило (элементарное преобразование): к строке определителя можно прибавить другую строку, умноженную на число, отличное от нуля. При этом значение определителя не изменится. «Другая строка» (которую прибавляЮТ) остаётся неизменной – и это в точности строка с числом-«мишенью»: Прочитайте и осмыслите это действие несколько раз! Далее. Чтобы получить ноль справа внизу, МЫСЛЕННО или НА ЧЕРНОВИКЕ умножаем вторую строку на 3: (6, –3, 3) и к третьей строке прибавляем вторую строку, умноженную на 3 (смотрим и вычисляем снизу вверх): 2) Путь второй. Организуем два нуля во второй строке: Столбец, который прибавляЮТ, остаётся неизменным, и это столбец с «синим» числом-«мишенью»: Теперь получим ещё один ноль. Для этого нужно к первому столбцу прибавить третий столбец, умноженный (мысленно или на черновике) на –2: Результат, естественно, получился тот же самый. А сейчас ВНИМАТЕЛЬНО и со всей ответственностью (!) прорешиваем аналогичную задачу Пример 74 Вычислить тот же определитель Полное решение и краткие комментарии в конце книги. Кстати, решение удобно контролировать с помощью приложенного к книге Матричного калькулятора: получили новую строку или столбец и сразу занесли её в Эксель. Если определитель изменил значение, значит, допущена ошибка. И заметьте, что нет никакой необходимости переставлять строки или столбцы. Элементарные преобразования прекрасно работают как слева направо, так и справа налево. Как сверху вниз, так и снизу вверх. По возможности выбирайте то, что вам удобнее, у начинающих популярны «мишени» в первой строке, т. к. её используют в методе Гаусса. Иногда в определителе отсутствует единица либо –1, например: В этом случае «мишень» следует организовать с помощью дополнительного элементарного преобразования. Сделать это можно обычно несколькими способами. Например, к первой строке прибавим вторую строку, умноженную (мысленно) на –1: ! Внимание: НЕ НУЖНО из первой строки вычитать вторую строку, это значительно увеличивает вероятность ошибки. Только складываем! К первой строке прибавляем вторую строку, умноженную –1. Именно так! Единица получена, чего и требовалось достичь. Но в некоторых случаях удаётся обойтись вообще без единиц, догадайтесь сами: Пример 75 Вычислить определитель, понизив его порядок: Метод понижения порядка становится особенно актуальным, а порой и просто спасительным, для определителей «четыре на четыре», «пять на пять» и выше. Вспомним Пример 57: И поэтому здесь можно (и нужно) свести решение к вычислению одного определителя «три на три». Единиц-«мишеней» тут много, и наша задача выбрать лучший вариант. Снова вспоминаем золотое правило: в строке (столбце) нулей должно быть побольше, а числа – поменьше. По этой причине нам подходит вторая строка либо четвёртый столбец. Четвёртый столбец выглядит привлекательнее, причём, там даже две единицы. В качестве «мишени» несколько удобнее выбрать элемент Первая строка не изменится. И вторая тоже – там уже есть нужный ноль: К третьей строке прибавим первую строку, умноженную (мысленно или на черновике) на –1 (смотрим и считаем снизу вверх): ! Внимание ещё раз: не нужно из третьей строки ВЫЧИТАТЬ первую строку. Только складываем! Результат записываем в третью строку: К четвёртой строке прибавим первую строку, умноженную (мысленно или на черновике) на 3 (смотрим и считаем снизу вверх): Результат записываем в четвёртую строку: Закомментирую дальнейшие действия: (1) Раскрываем определитель по четвёртому столбцу. Не забываем, что к элементу (2) В принципе, его можно разложить по строке (или столбцу), но мы отработаем свойства определителя. Вносим минус во вторую строку. (3) Ко второй строке прибавим первую строку, умноженную на 3. К третьей строке прибавим первую строку, умноженную на 7. (4) Раскрываем определитель по второму столбцу, тем самым ещё раз понижая его порядок до двух. Заметьте, как сократилось решение! Главное, немного «набить руку» на элементарных преобразованиях, и такая возможность вам представится прямо сейчас: Пример 76 Вычислить определитель двумя способами: а) получив нули в 3-й строке относительно элемента б) получив нули в 1-й строке относительно элемента Образец для сверки в конце книги. …Чем-то напоминает мне эта глава контрастный душ – то матрицы, то определители, то матрицы, то определители, матрицы, определители, и снова матрицы:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих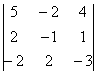
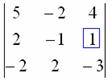
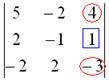
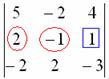
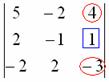
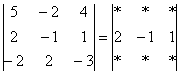
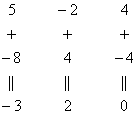
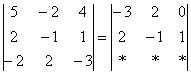
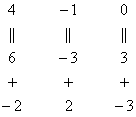
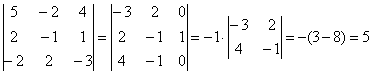
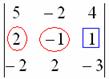
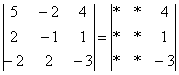
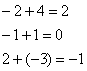
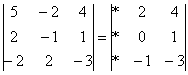
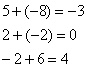
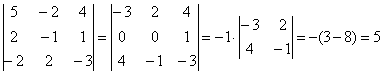
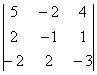 , выбрав в качестве числа-«мишени» элемент
, выбрав в качестве числа-«мишени» элемент 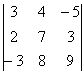 .
. 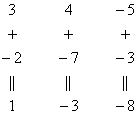
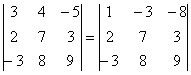
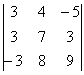
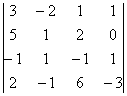 – сколько времени мы потратили на вычисления?!
– сколько времени мы потратили на вычисления?!
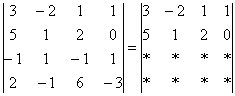
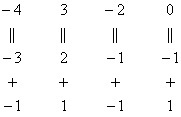
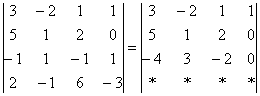
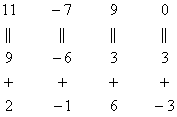
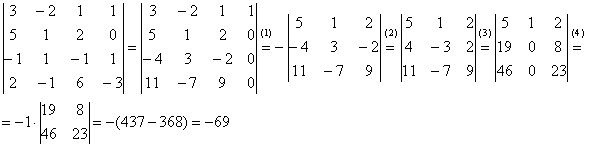
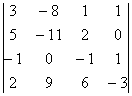
 4.13. Матричные уравнения
4.13. Матричные уравнения 4.11.5. Когда определитель равен нулю?
4.11.5. Когда определитель равен нулю?