|
Ваш репетитор, справочник и друг!
|
4.14.5. Элементарные преобразования матрицыОдно такое преобразование (причём, самое сложное) мы уже использовали для понижения порядка определителя, и пришло время систематизировать материал. Элементарные преобразования работают как для строк, так и для столбцов, но для определённости я буду говорить о привычных строках, и говорить в прикладном стиле. 1) Нулевую строку можно (и нужно) удалить из матрицы: 2) Если матрице есть пропорциональные (в частности одинаковые) строки, то достаточно оставить только одну из них. В нашем примере пропорциональны 2-я и 3-я строки, поэтому 2-ю строку (где числа по модулю больше) целесообразно удалить: Следует отметить, что нулевые и пропорциональные строки могут не только быть в матрице изначально, но и появиться в результате других элементарных преобразований. 3) Любые две строки можно поменять местами, например: 4) Строку (все её элементы) можно умножить на любое число, отличное от нуля. Умножим первую строку на –1, а вторую – на 1/2 (разделим на два): 5) И то самое, «сложное» преобразование. К строке можно прибавить другую строку, умноженную на любое ненулевое число. Результат записывается ВМЕСТО строки, к которой прибавляли, а «другая строка» остаётся неизменной. Возьмём ту же матрицу И перед тем как продолжить, подчеркну один важный момент. Если в нашем распоряжении есть произвольная матрица, то с ней ничего не нужно делать «просто так». И в самом деле, ведь в матрице может находиться какая-то ценная информация. Матрицу имеет смысл видоизменять дополнительно – лишь с какой-то целью. И сейчас наша цель – нахождение ранга. Тем более, есть такой замечательный факт: элементарные преобразования не меняют ранг матрицы
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих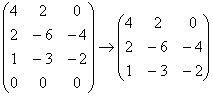 , если только сама матрица – не нулевая строка.
, если только сама матрица – не нулевая строка. 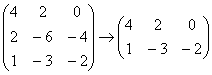

 4.14.6. Как найти ранг матрицы с помощью элементарных преобразований?
4.14.6. Как найти ранг матрицы с помощью элементарных преобразований? 4.14.4. Метод окаймляющих миноров
4.14.4. Метод окаймляющих миноров