|
Ваш репетитор, справочник и друг!
|
4.4. Умножение матрицЧем дальше в лес, тем толще партизаны. Скажу сразу, что правило умножения матриц выглядит весьма странно, впрочем, оставим лирику. Вопрос первый: какие матрицы можно умножать? Матрицу можно умножить на матрицу только в том случае, если количество столбцов 1-й матрицы равно количеству строк 2-й матрицы. Так, например, можно ли умножить матрицу Сканируем условие: Число столбцов 1-й матрицы равно числу строк 2-й матрицы, значит, умножение осуществимо. А вот если переставить матрицы местами, то
умножение уже аминь: Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно. Это, к слову, относится и к некоторым другим действиям с матрицами. Однако в ряде случаев можно умножать и так и так. Так, например, для матриц Вопрос второй: как перемножить две матрицы? Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение и общая формула введет в замешательство (или помешательство) большинство читателей. Начнём с самого простого: Пример 49 Умножить матрицу Умножение осуществляется по формуле Пример 50 Умножить матрицу Здесь формула такова: Считаем: Задание: самостоятельно выполнить матричное умножение Ну и, наверное, вы обратили внимание, что В общем случае матрицы переставлять нельзя! То есть, в отличие от чисел матричное умножение некоммутативно. Таким образом, если в задании предложено
умножить матрицу Однако существуют исключения из правила, и с одним из них я познакомлю вас прямо сейчас: Едем дальше. У начинающих часто возникает путаница с размерностью итоговой матрицы. Пожалуйста, перепишите к себе в тетрадь общую
схему: Пример 51 Выполнить матричное умножение Во-первых, проверим, можно ли вообще умножать. Число столбцов 1-й матрицы равно двум и число строк 2-й матрицы тоже равно двум, следовательно, всё ОК. Согласно схеме выше, в результате умножения должна получиться матрица «один на два», то есть строка из двух чисел. Вспоминаем наш мнемонический приём: сначала берём 1-й столбец правой матрицы, «поворачиваем
его на левый бок» и «пристраиваем» к единственной строке левой матрицы. Затем то же самое проделываем со 2-м столбцом: Самостоятельно: Пример 52
Сверяемся с решением и продолжаем набивать руку на типовых примерах: Пример 53 Умножить матрицу Формула очень похожа на аналогичный двумерный случай (Пример 49): В данном случае: И всего то. А теперь попробуйте самостоятельно разобраться в такой задачке: Пример 54 Умножьте матрицу Это очень распространённое произведение. Классика жанра Что делаем? Последовательно «перебираем» столбцы матрицы И ещё один практический секрет, не помню, кто сформулировал эту полезность: Приступая к выполнению задания, неплохо бы заранее знать результат Поэтому к книге приложен Матричный калькулятор – перед ручными расчётами просто забейте в него исходные матрицы и получИте правильный ответ. Это позволит контролировать каждый шаг вычислений и не пропустить возможные ошибки.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих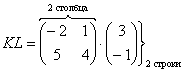
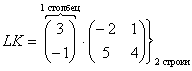
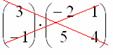
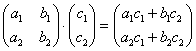 :
: 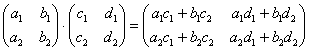 – попытайтесь сразу
уловить закономерность: сначала мы берём столбец «цэ», «поворачиваем его на левый бок» и «пристраиваем» к каждой строке 1-й матрицы. Затем
берём столбец «дэ» и аналогично «пристраиваем» его к каждой строке 1-й матрицы.
– попытайтесь сразу
уловить закономерность: сначала мы берём столбец «цэ», «поворачиваем его на левый бок» и «пристраиваем» к каждой строке 1-й матрицы. Затем
берём столбец «дэ» и аналогично «пристраиваем» его к каждой строке 1-й матрицы.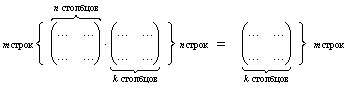
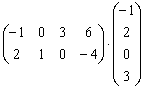
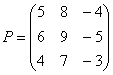 на матрицу
на матрицу 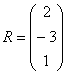
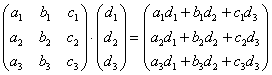
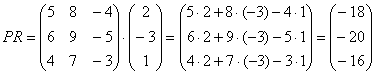
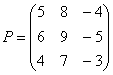 на матрицу
на матрицу 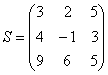
 4.5. Определитель матрицы
4.5. Определитель матрицы 4.3.4. Сумма (разность) матриц
4.3.4. Сумма (разность) матриц