1.8.1. Линейная независимость векторов плоскости. Базис.
Аффинная система координат на плоскости
Не пугаемся :) Всё разберём по порядку:
Рассмотрим плоскость вашего компьютерного стола (просто стола, тумбочки, пола, потолка, кому что нравится). Задача будет состоять в следующих действиях:
1) Выбрать базис плоскости. Грубо говоря, у столешницы есть длина и ширина, поэтому интуитивно понятно, что для построения базиса потребуется два вектора. Одного вектора явно мало, три вектора – лишка.
2) На основе выбранного базиса задать систему координат, чтобы присвоить координаты всем находящимся на столе предметам.
Не удивляйтесь, сначала объяснения будут на пальцах. Причём, на ваших. Пожалуйста, поместите указательный палец левой руки на край столешницы так, чтобы он смотрел в монитор. Это будет вектор 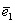 . Теперь поместите мизинец правой руки на край стола точно так же – чтобы он был направлен на экран монитора. Это будет вектор . Теперь поместите мизинец правой руки на край стола точно так же – чтобы он был направлен на экран монитора. Это будет вектор 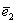 . …Улыбнитесь, вы замечательно выглядите! Что можно сказать о векторах . …Улыбнитесь, вы замечательно выглядите! Что можно сказать о векторах 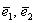 ? Данные векторы коллинеарны, а значит, линейно (через множитель-константу) выражаются друг через друга: ? Данные векторы коллинеарны, а значит, линейно (через множитель-константу) выражаются друг через друга:
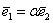 , ну, или наоборот: , ну, или наоборот: 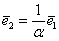 , где , где 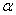 – некоторое число, отличное от нуля. – некоторое число, отличное от нуля.
Картинку сего действа мы видели, когда умножали вектор на число.
Будут ли ваши пальчики 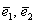 задавать базис на плоскости компьютерного стола? Очевидно, что нет. Коллинеарные векторы путешествуют туда-сюда по одному направлению, а у плоскости есть длина и ширина. Такие векторы называют линейно зависимыми. Два вектора плоскости линейно зависимы тогда и только тогда они коллинеарны. задавать базис на плоскости компьютерного стола? Очевидно, что нет. Коллинеарные векторы путешествуют туда-сюда по одному направлению, а у плоскости есть длина и ширина. Такие векторы называют линейно зависимыми. Два вектора плоскости линейно зависимы тогда и только тогда они коллинеарны.
Скрестите пальцы на столе, чтобы между ними был любой угол, кроме 0 или 180 градусов. Два вектора плоскости 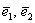 линейно независимы в том и только том случае, если они не коллинеарны. Итак, базис линейно независимы в том и только том случае, если они не коллинеарны. Итак, базис 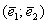 получен. Не нужно смущаться, что он получился «косым» с неперпендикулярными векторами разной длины. Очень скоро мы увидим, что для его построения пригоден не только угол в 90 градусов, и не только единичные, равные по длине векторы. получен. Не нужно смущаться, что он получился «косым» с неперпендикулярными векторами разной длины. Очень скоро мы увидим, что для его построения пригоден не только угол в 90 градусов, и не только единичные, равные по длине векторы.
Любой вектор плоскости 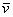 единственным образом раскладывается по базису единственным образом раскладывается по базису 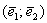 : :
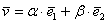 , где , где 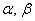 – действительные числа. Числа – действительные числа. Числа 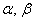 называют координатами вектора в данном базисе. называют координатами вектора в данном базисе.
Также говорят, что вектор 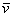 представлен в виде линейной комбинации базисных векторов. То есть, выражение представлен в виде линейной комбинации базисных векторов. То есть, выражение 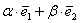 называют разложением вектора называют разложением вектора 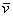 по базису по базису 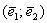 или линейной комбинацией базисных векторов. или линейной комбинацией базисных векторов.
Так, можно сказать, что вектор 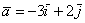 разложен по ортонормированному базису разложен по ортонормированному базису 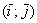 , а можно сказать, что он представлен в виде линейной комбинации векторов , а можно сказать, что он представлен в виде линейной комбинации векторов 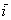 и и 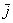 . .
Сформулируем определение базиса формально:
Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов 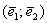 , взятых в определённом порядке, при этом любой вектор плоскости является линейной комбинацией базисных векторов. , взятых в определённом порядке, при этом любой вектор плоскости является линейной комбинацией базисных векторов.
Существенным моментом определения является тот факт, что векторы взяты в определённом порядке. Базисы 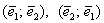 – это два совершенно разных базиса! Как говорится, мизинец левой руки не переставишь на место мизинца правой руки. – это два совершенно разных базиса! Как говорится, мизинец левой руки не переставишь на место мизинца правой руки.
Хорошо, с базисом разобрались, но его недостаточно, чтобы присвоить координаты каждому предмету вашего компьютерного стола. Почему недостаточно? Векторы являются свободными и блуждают по всей плоскости. Поэтому нужен отправной ориентир,
и в роли такого ориентира выступает начало координат – это точка с координатами 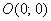 , задающая начало отсчёта. В качестве начала координат мы можем выбрать любую точку плоскости, и располагаться она может хоть на краю Вселенной. , задающая начало отсчёта. В качестве начала координат мы можем выбрать любую точку плоскости, и располагаться она может хоть на краю Вселенной.
Начало координат 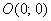 и неколлинеарные векторы и неколлинеарные векторы 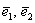 , взятые в определённом порядке (базис), задают аффинную систему координат плоскости: , взятые в определённом порядке (базис), задают аффинную систему координат плоскости:
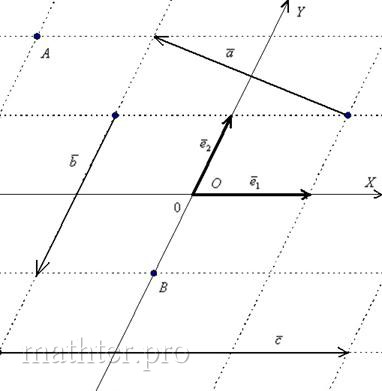
Иногда такую систему координат называют косоугольной системой. В качестве примеров на чертеже изображены точки 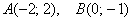 и векторы: и векторы:
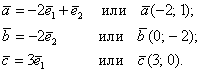
В аффинной системе координат перестают работать некоторые формулы, которые мы рассмотрели ранее, в частности, формулы вычисления длин.
…вы скажете неудобная система? Всё относительно! – да и рептилоиды с планеты Небиру одобряют :) Но мы, конечно, с ними не согласны:
Начало координат и два ортогональных вектора 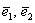 произвольной ненулевой длины задают ортогональную систему координат: произвольной ненулевой длины задают ортогональную систему координат:
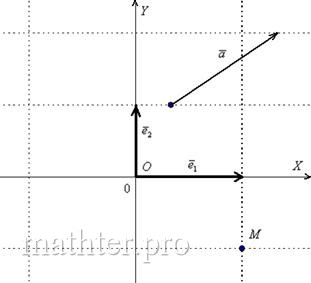
В качестве примера на чертеже изображена точка 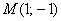 и вектор и вектор 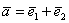 (или (или 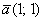 ). Очевидное неудобство этого базиса состоит в том, что координатные векторы в общем случае имеют разные длины и не равны единице. А если они единичные, то получается привычная прямоугольная (декартова) система координат, которая определяется началом координат ). Очевидное неудобство этого базиса состоит в том, что координатные векторы в общем случае имеют разные длины и не равны единице. А если они единичные, то получается привычная прямоугольная (декартова) система координат, которая определяется началом координат 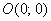 и ортонормированным базисом и ортонормированным базисом 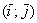 : :
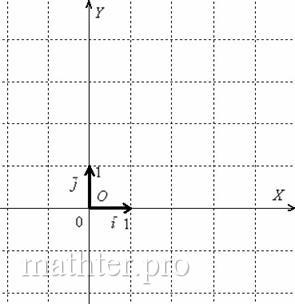
Ось 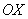 называют осью абсцисс, а ось называют осью абсцисс, а ось 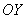 – осью ординат. Чтобы задать размерность достаточно поставить нолик и две единички по осям. НЕ НУЖНО использовать «сплошную» нумерацию: – осью ординат. Чтобы задать размерность достаточно поставить нолик и две единички по осям. НЕ НУЖНО использовать «сплошную» нумерацию:  Ибо координатная плоскость – не памятник Декарту, а студент – не голубь :) Ибо координатная плоскость – не памятник Декарту, а студент – не голубь :)
Популярные «тетрадные» масштабы: 1 ед. = 1 клетка или 1 ед. = 2 клетки.
Следует отметить, что декартову систему координат можно определить не только через векторы, и во многих задачах векторы 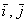 не чертят. не чертят.
Переходим к практической части. Все задачи этого параграфа справедливы как для «школьной» системы координат, так и для общего аффинного случая; ничего сложного:
 1.8.2. Как определить коллинеарность векторов плоскости? 1.8.2. Как определить коллинеарность векторов плоскости?
 1.7.2. Проекции вектора на координатные оси. Направляющие косинусы 1.7.2. Проекции вектора на координатные оси. Направляющие косинусы
| Оглавление |
|