1.7.2. Проекции вектора на координатные оси.
Направляющие косинусы
Рассмотрим вектор плоскости 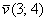 , заданный своими
координатами в ортонормированном базисе , заданный своими
координатами в ортонормированном базисе 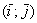 . Для
удобства я отложу его от начала координат: . Для
удобства я отложу его от начала координат:

Проекцией вектора 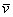 на координатную ось на координатную ось 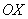 является в точности его первая координата: является в точности его первая координата: 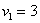 (красная черта). Обозначим через (красная черта). Обозначим через 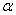 угол между вектором угол между вектором 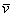 и координатным вектором и координатным вектором 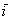 : : 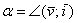 (красная дуга). По определению косинуса: (красная дуга). По определению косинуса:
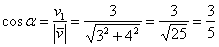
Аналогично со второй координатой: проекцией вектора 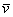 на координатную ось на координатную ось 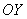 является его вторая координата: является его вторая координата: 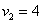 (малиновая черта). Обозначим через (малиновая черта). Обозначим через 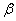 угол между вектором угол между вектором 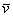 и координатным вектором и координатным вектором 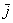 : : 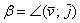 (двойная
малиновая дуга). Тогда: (двойная
малиновая дуга). Тогда: 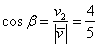
Косинусы 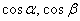 называются направляющими косинусами
вектора. Причём, для любого ненулевого вектора справедливо равенство называются направляющими косинусами
вектора. Причём, для любого ненулевого вектора справедливо равенство 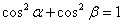 . Проверим его справедливость для рассматриваемого вектора: . Проверим его справедливость для рассматриваемого вектора:
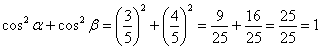 , что и требовалось проверить. , что и требовалось проверить.
Заметьте, что приведённые выше выкладки не изменятся, если вектор 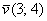 отложить от любой другой точки плоскости отложить от любой другой точки плоскости
Итак, направляющие косинусы ненулевого вектора 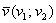 , заданного в ортонормированном базисе , заданного в ортонормированном базисе 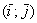 , выражаются формулами , выражаются формулами 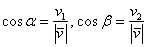 , а сами координаты вектора можно выразить через его длину и данные
косинусы: , а сами координаты вектора можно выразить через его длину и данные
косинусы:
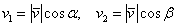 , то есть: , то есть: 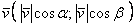 . .
Вектор же с координатами 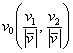 – это в точности единичный вектор, сонаправленный с вектором – это в точности единичный вектор, сонаправленный с вектором 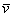 . .
С пространственными векторами, заданными в ортонормированном базисе 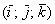 , разборки такие же. Рассмотрим произвольный ненулевой вектор , разборки такие же. Рассмотрим произвольный ненулевой вектор 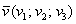 . Его координаты представляют собой проекции вектора на оси . Его координаты представляют собой проекции вектора на оси 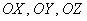 соответственно. Обозначим углы данного
вектора с ортами через: соответственно. Обозначим углы данного
вектора с ортами через: 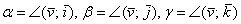 . Тогда направляющие
косинусы вектора выражаются формулами: . Тогда направляющие
косинусы вектора выражаются формулами:
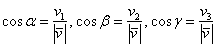 , ,
при этом справедливо равенство 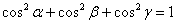 . .
Вектор 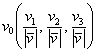 – есть единичный вектор, сонаправленный с вектором – есть единичный вектор, сонаправленный с вектором 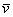 . .
В практических задачах чаще всего требуется найти направляющие косинусы вектора, заключительный пример параграфа:
Задача 36
Найти направляющие косинусы векторов:
а) 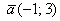 , проверить, что , проверить, что 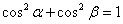 ; ;
б) 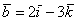 , проверить, что , проверить, что 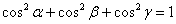 . .
Направляющий косинусы можно найти по прямым формулам, либо сначала найти единичные векторы, и затем сослаться на тот факт,
что их координаты – это соответствующие направляющие косинусы.
Решите эту задача самостоятельно! И, конечно, с проверкой, ибо без неё грех.
 1.8.1. Базис и система координат на плоскости 1.8.1. Базис и система координат на плоскости
 1.7.1. Как найти проекцию вектора на вектор? 1.7.1. Как найти проекцию вектора на вектор?
| Оглавление |
|