1.7.1. Как найти проекцию вектора на вектор?
Рассмотрим ненулевые векторы 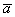 и и 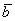 : :
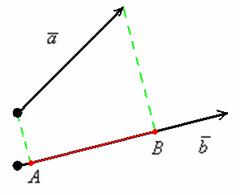
Спроецируем вектор 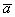 на вектор на вектор 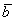 , для этого из начала и конца вектора , для этого из начала и конца вектора 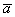 опустим перпендикуляры на вектор опустим перпендикуляры на вектор 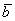 (зелёные пунктирные линии). (зелёные пунктирные линии).
Представьте,
что на вектор 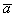 перпендикулярно сверху падают
лучи света. Тогда отрезок перпендикулярно сверху падают
лучи света. Тогда отрезок 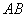 будет «тенью»
вектора будет «тенью»
вектора 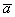 . Проекцией вектора . Проекцией вектора 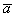 на вектор на вектор 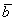 является ДЛИНА отрезка является ДЛИНА отрезка 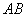 . То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО. . То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
Это ЧИСЛО обозначается следующим образом: 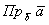 , «большим вектором» обозначают вектор КОТОРЫЙ проецируют,
«маленьким подстрочным вектором» обозначают вектор НА который проецируют. , «большим вектором» обозначают вектор КОТОРЫЙ проецируют,
«маленьким подстрочным вектором» обозначают вектор НА который проецируют.
Сама запись 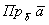 читается так: «проекция
вектора «а» на вектор «бэ»». читается так: «проекция
вектора «а» на вектор «бэ»».
Если угол между векторами 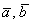 острый (как на рисунке выше), то острый (как на рисунке выше), то 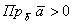
Если векторы 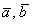 ортогональны, то ортогональны, то 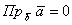 (проекцией является точка, размеры которой считаются нулевыми). (проекцией является точка, размеры которой считаются нулевыми).
Если угол между векторами 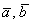 тупой (на рисунке мысленно переставьте стрелочку вектора тупой (на рисунке мысленно переставьте стрелочку вектора 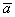 ), то ), то 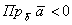 (та же длина с добавленным знаком «минус»). (та же длина с добавленным знаком «минус»).
Отвечу на назревший вопрос: что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую
вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ», попросту – на прямую, содержащую
вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на
прямую, содержащую вектор «бэ».
Из вышесказанного следует, что проекция вектора 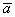 на любой ненулевой сонаправленный вектор на любой ненулевой сонаправленный вектор
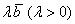 будет точно такой же: будет точно такой же:
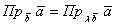 – фактически это проекция вектора – фактически это проекция вектора
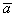 на прямую на прямую 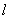 , которая содержит сонаправленные векторы , которая содержит сонаправленные векторы 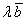 (и поскольку векторы свободны, то таких прямых будет
бесконечно много, все они будут параллельны друг другу); (и поскольку векторы свободны, то таких прямых будет
бесконечно много, все они будут параллельны друг другу);
а если векторы направлены противоположно 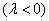 , то
добавится знак «минус»: , то
добавится знак «минус»:
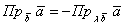
Отложим наши подопытные векторы от одной точки:
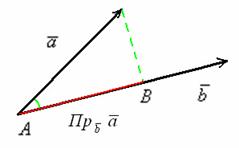
и рассмотрим прямоугольный треугольник. Косинус угла 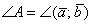 – есть отношение прилежащего катета к гипотенузе: – есть отношение прилежащего катета к гипотенузе:
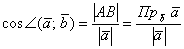 , но с другой стороны, у нас уже получена
формула косинуса угла между векторами: , но с другой стороны, у нас уже получена
формула косинуса угла между векторами:
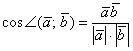
…все ли догадались, что будет дальше?
Приравниваем формулы:
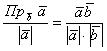
и сокращаем знаменатели обеих частей на 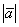 ,
получая формулу для вычисления проекции: ,
получая формулу для вычисления проекции:
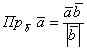
Распишем её в координатах:
Если векторы плоскости 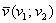 и и 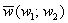 заданы в ортонормированном базисе заданы в ортонормированном базисе 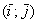 , то проекция вектора , то проекция вектора 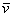 на вектор на вектор 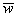 выражается формулой: выражается формулой:
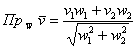
Если векторы пространства 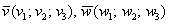 заданы в ортонормированном базисе заданы в ортонормированном базисе 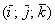 , то проекция вектора , то проекция вектора 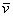 на вектор на вектор 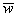 выражается формулой: выражается формулой:
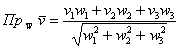
Легко убедиться, что проекция вектора 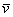 на
коллинеарный вектор на
коллинеарный вектор 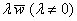 может
отличаться лишь знАком, приведу выкладки для «плоского» случая может
отличаться лишь знАком, приведу выкладки для «плоского» случая 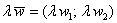 : :
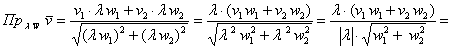
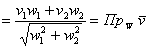 , если , если 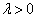 , и , и 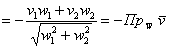 , если , если 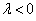
Задача 34
Найти проекцию вектора 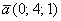 на вектор на вектор 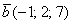
Решение в одну строчку:
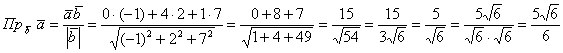 , на завершающем шаге я умножил числитель и
знаменатель на , на завершающем шаге я умножил числитель и
знаменатель на 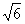 , избавившись тем самым от
иррациональности в знаменателе. , избавившись тем самым от
иррациональности в знаменателе.
Ответ: 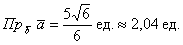
Проекция – это ДЛИНА, поэтому обязательно указываем размерность, правда, если получится знак «минус», то смотреться это
будет своеобразно.
Задача 35
Треугольник задан своими вершинами 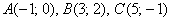 .
Найти: .
Найти:
а) проекцию стороны 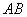 на сторону на сторону 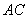 ; ;
б) проекцию стороны 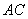 на сторону на сторону 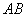 . .
Это задача для самостоятельного решения.
Итак, как найти проекцию вектора 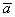 на отрезок с известными концами на отрезок с известными концами 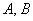 ? (как вариант, на продолжение этого отрезка). Находим вектор ? (как вариант, на продолжение этого отрезка). Находим вектор 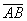 и используем формулу и используем формулу 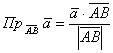 . Либо вектор . Либо вектор 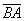 и формулу и формулу 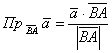 . В
одном из случаев получится отрицательное значение, и если оно вас напрягает, выберите другой вариант :) . В
одном из случаев получится отрицательное значение, и если оно вас напрягает, выберите другой вариант :)
О проекции же вектора на прямую поговорим в следующей главе, а пока
выясним геометрический смысл координат векторов в ортонормированном базисе:
 1.7.2. Проекции вектора на координатные оси. Направляющие косинусы 1.7.2. Проекции вектора на координатные оси. Направляющие косинусы
 1.6.9. Как найти угол между векторами в координатах? 1.6.9. Как найти угол между векторами в координатах?
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»

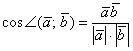
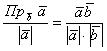
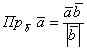
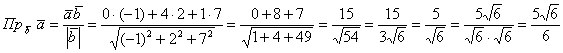 , на завершающем шаге я умножил числитель и
знаменатель на
, на завершающем шаге я умножил числитель и
знаменатель на 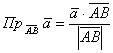 . Либо вектор
. Либо вектор 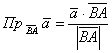 . В
одном из случаев получится отрицательное значение, и если оно вас напрягает, выберите другой вариант :)
. В
одном из случаев получится отрицательное значение, и если оно вас напрягает, выберите другой вариант :) 1.7.2. Проекции вектора на координатные оси. Направляющие косинусы
1.7.2. Проекции вектора на координатные оси. Направляющие косинусы 1.6.9. Как найти угол между векторами в координатах?
1.6.9. Как найти угол между векторами в координатах?