|
Ваш репетитор, справочник и друг!
|
1.6.9. Как найти угол между векторами в координатах?Теперь у нас есть полная информация, чтобы ранее выведенную формулу косинуса
угла между векторами Косинус угла между векторами плоскости Косинус угла между векторами пространства Возвращаемся к нашим треугольникам: Задача 31 Даны три вершины треугольника Решение: по условию чертёж выполнять не требуется, но всё-таки: Вычислим скалярное произведение: Таким образом: Именно такой порядок выполнения задания рекомендую «чайникам». Более подготовленные читатели могут записать вычисления
«одной строкой»: Косинус получился «плохим» (не табличным), однако, это не окончательный ответ задачи, и поэтому, к слову, не имеет особого смысла избавляться от корня в знаменателе. Найдём сам угол: Если посмотреть на чертёж, то результат вполне правдоподобен. Для проверки можно использовать Алгебраический Калькулятор (см. Приложения) или даже измерить угол транспортиром (у кого он есть). Только не повредите покрытие монитора =) Ответ: Задача 32 В пространстве задан треугольник координатами своих вершин Это пример для самостоятельного решения, и, конечно же, задачка творческая, повторяем взаимосвязь между углом и знаком скалярного произведения: Задача 33 При каком значении Решение и ответ в конце книги. Следующий небольшой параграф будет посвящен ортогональным проекциям векторов, в которых тоже «замешано» скалярное произведение:
|
|
© mathprofi.ru - mathter.pro, 2010-2025, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»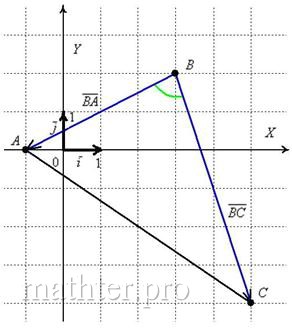
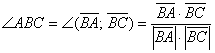 , и дальнейшее понятно. Найдём векторы и их длины:
, и дальнейшее понятно. Найдём векторы и их длины: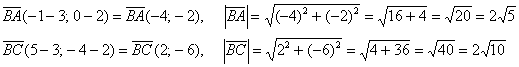
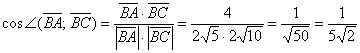
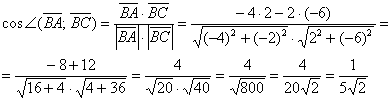
 1.7.1. Как найти проекцию вектора на вектор?
1.7.1. Как найти проекцию вектора на вектор? 1.6.8. Если векторы заданы суммами векторов с известными координатами
1.6.8. Если векторы заданы суммами векторов с известными координатами