|
Ваш репетитор, справочник и друг!
|
1.6.5. Как найти угол между векторами?Снова посмотрим на нашу формулу В чём смысл этой формулы? Если известны длины двух векторов и их скалярное произведение, то можно вычислить косинус угла
между данными векторами, а, следовательно, и сам угол – с помощью обратной функции Задача 21 Найти угол между векторами Решение: используем формулу: На заключительном этапе вычислений использован технический приём – устранение иррациональности в
знаменателе. В целях устранения иррациональности я домножил числитель и знаменатель на Итак, если Значения обратных тригонометрических функций можно находить по соответствующей тригонометрической таблице (см.
Приложение Тригонометрия). Но гораздо чаще появляется какой-нибудь неуклюжий медведь вроде Ответ: Опять – не забываем указывать размерность, радианы и градусы. Лично я, чтобы заведомо «снять все вопросы», предпочитаю указывать и то, и то (если по условию, конечно, не требуется представить ответ только в радианах или только в градусах). Теперь вы сможете самостоятельно справиться с более сложным заданием: Задача 22 Даны Разберём алгоритм решения: 1) По условию требуется найти угол между векторами 2) Находим скалярное произведение 3) Находим длину вектора 4) Концовка решения совпадает с Задачей 22. Краткое решение и ответ в конце книги.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»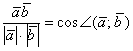 , а части поменяем местами:
, а части поменяем местами: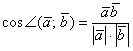
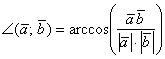 .
.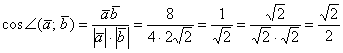
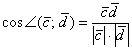 .
. 1.6.6. Скалярное произведение векторов в координатах
1.6.6. Скалярное произведение векторов в координатах 1.6.4. Свойства скалярного произведения
1.6.4. Свойства скалярного произведения