|
Ваш репетитор, справочник и друг!
|
1.6.4. Свойства скалярного произведенияДля произвольных векторов 1) 2) 3) Зачастую всевозможные свойства (которые ещё и доказывать надо!) воспринимаются студентами как ненужный хлам, который лишь
необходимо вызубрить и сразу после экзамена благополучно забыть. Казалось бы, чего тут важного – все и так с первого класса
знают, что от перестановки множителей произведение не меняется: Задача 17 Найти скалярное произведение векторов Решение: сначала проясним ситуацию с вектором Итак, по условию требуется найти скалярное произведение
(1) Поставляем выражения векторов (2) Используя дистрибутивное свойство, раскрываем скобки по правилу умножения многочленов: чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена. (3) В первом и последнем слагаемом компактно записываем скалярные квадраты векторов: (4) Приводим подобные слагаемые: (5) В первом слагаемом используем формулу скалярного квадрата (6) Подставляем исходные данные Ответ: Отрицательное значение скалярного произведения констатирует тот факт, что угол между векторами Задача типовая, вот пример для самостоятельного решения: Задача 18 Найти скалярное произведение векторов Теперь ещё одно распространённое задание, как раз на новую формулу длины вектора Задача 19 Найти длину вектора Сначала решение, затем комментарии:
(1) Поставляем выражение вектора (2) Используем формулу длины: (3) Используем школьную формулу квадрата суммы (4) Дальнейшее уже знакомо из двух предыдущих задач. Ответ: Коль скоро речь шла о длине, то не забываем указать размерность – «единицы». Задача 20 Найти длину вектора Это пример для самостоятельного решения. Продолжаем выжимать полезные вещи из скалярного произведения:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»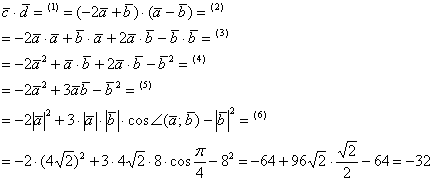
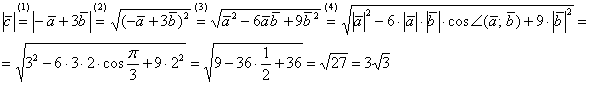
 1.6.5. Как найти угол между векторами?
1.6.5. Как найти угол между векторами? 1.6.3. Скалярный квадрат вектора
1.6.3. Скалярный квадрат вектора