1.6.1. Определение скалярного произведения

Сложение векторов, умножение вектора на число…. Было бы наивным думать, что этой всё. Приоткроем же, наконец, дверь и увлечённо посмотрим, что происходит, когда два вектора встречают друг друга…. Нижеследующие понятия, факты и задачи справедливы как для векторов плоскости, так и для векторов пространства. Сначала выясним, как определяется

угол между векторами

Думаю, всем интуитивно понятно, что это такое, но, тем не менее: угол между двумя ненулевыми векторами и – это меньший угол между соответствующими направленными отрезками, отложенными от одной точки:

В литературе значок угла часто пропускают и пишут просто . Угол между векторами может принимать значения от 0 до 180 градусов (от 0 до радиан) включительно. Аналитически данный факт записывается в виде двойного неравенства: либо (в радианах).

Определение скалярного произведения

Скалярным произведением двух векторов и называется ЧИСЛО, равное произведению длин этих векторов на косинус угла между ними:

Акцентируем внимание на существенной информации:

Обозначение: скалярное произведение обозначается через или просто .

Результат операции является ЧИСЛОМ: умножается вектор на вектор, а получается число. Действительно, если длины векторов – это числа, косинус угла – число, то их произведение тоже будет числом.

Сразу пара разминочных примеров:

Задача 15

Найти скалярное произведение векторов и , если

Решение: используем формулу . В данном случае:

Ответ:

Значения косинуса можно найти в тригонометрической таблице (см. Приложение Тригонометрия), а если нужного значения там нет, то используйте калькулятор.

Чисто с математической точки зрения скалярное произведение безразмерно, то есть результат, в данном случае , просто число и всё. С точки же зрения задач физики скалярное произведение всегда имеет определенный физический смысл, то есть после результата нужно указать ту или иную физическую единицу. Каноничный пример – это вычисление работы силы . Работа силы измеряется в Джоулях, поэтому, и ответ запишется вполне конкретно, например, .

Задача 16

Найти , если , а угол между векторами равен .

Это пример для самостоятельного решения.

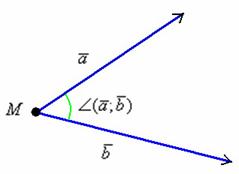
1.6.2. Угол между векторами и знак скалярного произведения

1.5.7. Формулы координат середины отрезка

| Оглавление |

Автор: Aлeксaндр Eмeлин