1.6.2. Угол между векторами и знак скалярного произведения
В Задаче 15 скалярное произведение получилось положительным, а в Задаче 16 – отрицательным. Выясним, от чего зависит знак
скалярного произведения. Смотрим на нашу формулу: 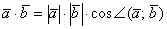 . Длины ненулевых векторов всегда положительны: . Длины ненулевых векторов всегда положительны: 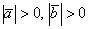 , поэтому знак может зависеть только от значения косинуса: , поэтому знак может зависеть только от значения косинуса:
1) Если угол между векторами острый: 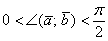 (от 0 до 90 градусов), то (от 0 до 90 градусов), то 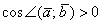 и скалярное произведение будет положительным: и скалярное произведение будет положительным: 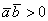 . Особый случай: если векторы сонаправлены, то угол между ними считается нулевым . Особый случай: если векторы сонаправлены, то угол между ними считается нулевым 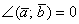 , и скалярное произведение также будет положительным. Поскольку , и скалярное произведение также будет положительным. Поскольку 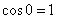 , то формула упрощается: , то формула упрощается: 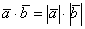 . .
2) Если угол между векторами тупой: 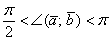 (от 90 до 180 градусов), то (от 90 до 180 градусов), то 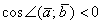 , и, соответственно, скалярное произведение отрицательно: , и, соответственно, скалярное произведение отрицательно: 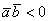 . Особый случай: если векторы направлены противоположно, то угол между ними считается развёрнутым: . Особый случай: если векторы направлены противоположно, то угол между ними считается развёрнутым: 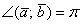 (180 градусов). Скалярное произведение здесь тоже отрицательно,
так как (180 градусов). Скалярное произведение здесь тоже отрицательно,
так как 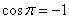 . .
Справедливы и обратные утверждения:
Если 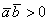 , то угол между данными векторами
острый, как вариант, векторы сонаправлены. Если , то угол между данными векторами
острый, как вариант, векторы сонаправлены. Если 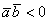 , то угол между данными векторами тупой, как вариант, векторы направлены
противоположно. , то угол между данными векторами тупой, как вариант, векторы направлены
противоположно.
Но особый интерес представляет третий случай:
3) Если угол между векторами прямой: 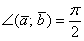 (90 градусов), то (90 градусов), то 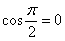 и скалярное произведение равно нулю: и скалярное произведение равно нулю: 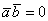 . Обратное тоже верно: если . Обратное тоже верно: если 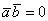 , то , то 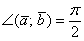 . Компактно утверждение формулируется так: скалярное произведение двух
векторов равно нулю тогда и только тогда, когда данные векторы ортогональны. Короткая математическая запись: . Компактно утверждение формулируется так: скалярное произведение двух
векторов равно нулю тогда и только тогда, когда данные векторы ортогональны. Короткая математическая запись: 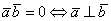 (т.е. из одного следует другое). (т.е. из одного следует другое).
Третий случай имеет большую практическую значимость, поскольку позволяет выяснить, ортогональны векторы или нет.
 1.6.3. Скалярный квадрат вектора 1.6.3. Скалярный квадрат вектора
 1.6.1. Определение скалярного произведения 1.6.1. Определение скалярного произведения
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников» 1.6.3. Скалярный квадрат вектора
1.6.3. Скалярный квадрат вектора 1.6.1. Определение скалярного произведения
1.6.1. Определение скалярного произведения