|
Ваш репетитор, справочник и друг!
|
1.9.1. Векторное произведение векторов. Определение и его смыслДанная операция определена для двух пространственных векторов, пусть это будут нетленные буквы Обозначение: И сразу вопрос: в чём отличие векторного произведения от произведения скалярного? Явное отличие, прежде всего, в РЕЗУЛЬТАТЕ: – Результатом скалярного произведения векторов является ЧИСЛО: – Результатом векторного произведения векторов является ВЕКТОР: В учебной
литературе обозначения тоже могут варьироваться, я буду использовать букву Определение: векторным произведением 1) Исходные векторы 2) Векторы 3)Геометрический смысл векторного произведения. Это очень важный пункт! ДЛИНА «синего» вектора Примечание: чертёж является схематическим, и поэтому номинальная длина векторного произведения не равна площади параллелограмма. Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними. Поэтому,
исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения: Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь
треугольника, построенного на векторах 4) Не менее важный факт состоит в том, что вектор 5) Вектор Итак, определение разобрано и осталось выяснить, что происходит, когда векторы Таким образом, если Справедливо и обратное: если Частный случай – векторное произведение вектора на самого себя: Ну что же, разжигаем огонь практики: Задача 46 а) Найти длину векторного произведения векторов б) Найти площадь параллелограмма, построенного на векторах Нет, это не опечатка! – исходные данные в пунктах условия я намеренно сделал одинаковыми. Чтобы подчеркнуть отличие в решениях: а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле: Для нахождения значений синуса удобно использовать соответствующую Тригонометрическую таблицу (см. Приложение Тригонометрия). Ответ: Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы. б) По условию требуется найти площадь параллелограмма, построенного на векторах
Ответ: Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры, соответственно, размерность – квадратные единицы. Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формируем чёткий ответ! В противном случае задание с высокой вероятностью вернётся на доработку, но это ещё не самое плохое. У рецензента может сложиться впечатление, что человек плохо разобрался в теме и его бы надо допросить с пристрастием :). Об этом нужно помнить, решая любую задачу по высшей математике, да и по другим предметам тоже. Типовая задача для самостоятельного решения: Задача 47 Найти площадь треугольника, построенного на векторах Формула нахождения площади треугольника дана в комментариях к определению векторного произведения (см. выше). Решение и ответ в конце книги. Для решения других задач нам понадобятся:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»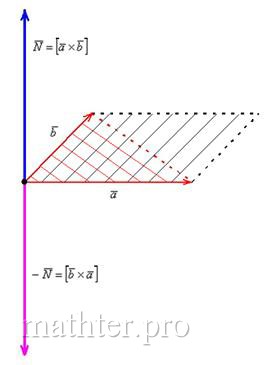 Разберём определение «по косточкам»:
Разберём определение «по косточкам»:  1.9.2. Свойства векторного произведения
1.9.2. Свойства векторного произведения 1.8.4. Базис и система координат пространства
1.8.4. Базис и система координат пространства