|
Ваш репетитор, справочник и друг!
|
1.8.4. Базис и система координат пространстваМногие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия. Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний. И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний
палец. Это будут векторы Кстати, не нужно демонстрировать такое преподавателям, как ни крути пальцами, а от определений никуда не деться =) Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными, и совершенно понятно, что базиса трёхмерного пространства они не создают. Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)). Определение: векторы называются компланарными, если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны. Три компланарных вектора всегда линейно зависимы, то есть линейно выражаются друг через друга. Для простоты снова
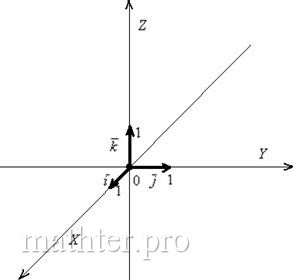
представим, что они лежат в одной плоскости. Во-первых, векторы Справедливо и противоположное утверждение: три некомпланарных вектора всегда линейно независимы, то есть никоим образом не выражаются друг через друга. И, очевидно, только такие векторы могут образовать базис трёхмерного пространства. Определение: базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки (начала отсчёта) и любых трёх линейно независимых векторов: Выбранное (где угодно) начало координат Ось абсцисс И перед тем как перейти к практическим заданиям, вновь систематизируем теоретическую информацию: Для трёх векторов пространства эквиваленты следующие утверждения: 1) векторы линейно независимы; Противоположные высказывания, думаю, понятны. Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5), и оставшиеся практические задания параграфа будут носить ярко выраженный алгебраический характер. Повесим на гвоздь геометрическую клюшку и начнём орудовать бейсбольной битой линейной алгебры: Три вектора пространства Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (результат не изменится). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач. Задача 42 Проверить, образуют ли векторы базис трёхмерного пространства: а) б) Фактически всё решение сводится к вычислению определителей: а) Вычислим определитель, составленный из координат векторов Ответ: данные векторы образуют базис. б) Это пункт для самостоятельного решения. Не пропускаем! Для проверки правильности вычислений определителей я приложил к книге Алгебраический Калькулятор. Решим творческую задачку: Задача 43 При каком значении параметра Решение: Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен
нулю: По существу, требуется решить уравнение с определителем. Определитель выгоднее всего раскрыть по второй строке: Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению: Ответ: при Здесь легко выполнить проверку, для этого нужно подставить полученное значение И в заключение параграфа рассмотрим ещё одну типовую задачу, которая встречается в подавляющем большинстве контрольных работ по алгебре и геометрии: Задача 44 Даны векторы Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе.
Какой это базис – нас не интересует. А интересует следующая вещь: три вектора ! Важно: координаты векторов Теперь вспомним теоретическую часть: если векторы Поскольку наши векторы И по условию требуется найти координаты Для удобства объяснения поменяю части местами: Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают по формулам Крамера, часто даже в условии задачи есть такое требование. Главный определитель системы уже найден: Дальнейшее дело техники: Таким образом: Ответ: Такая же задача для самостоятельного решения: Задача 45 Даны векторы Полное решение и примерный образец чистового оформления в конце книги. Для самоконтроля используйте тот же Алгебраический Калькулятор, где есть макет с автоматическим расчётом системы по правилу Крамера.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»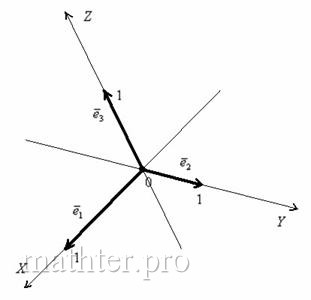
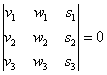 .
.
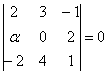
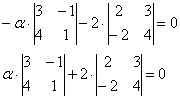
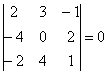 , раскрыв его заново.
, раскрыв его заново.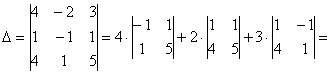
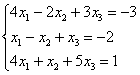 – коэффициенты левой части берём из опр-ля
– коэффициенты левой части берём из опр-ля 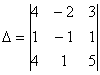 ,
, 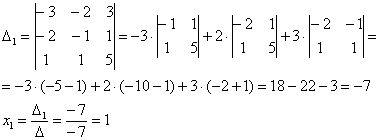
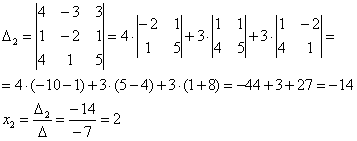
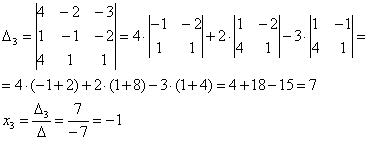
 1.9.1. Векторное произведение векторов. Определение и его смысл
1.9.1. Векторное произведение векторов. Определение и его смысл 1.8.3. Как определить коллинеарность векторов пространства?
1.8.3. Как определить коллинеарность векторов пространства?