1.8.3. Как определить коллинеарность векторов пространства?

Правило то же самое, только добавляется дополнительная координата:

Для того чтобы два вектора пространства были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны: ( – ненулевая константа).

Данная система представляет собой покоординатную роспись линейной зависимости этих векторов:

Задача 41

Выяснить, будут ли коллинеарны следующие векторы пространства:

а) ;

б) ;

в) .

Решение:

а) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:

Система не имеет решения, значит, векторы не коллинеарны.

«Упрощёнка» оформляется пропорцией . В данном случае:
– соответствующие координаты не пропорциональны, значит, векторы не коллинеарны.

Ответ: векторы не коллинеарны.

б-в) Это пункты для самостоятельного решения. Попробуйте его оформить двумя способами.

Существует и другой метод проверки пространственных векторов на коллинеарность – с помощью векторного произведения векторов.

Аналогично «плоскому» случаю, эти методы можно применять для исследования параллельности пространственных отрезков и прямых.

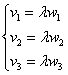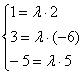
1.8.4. Базис и система координат пространства

1.8.2. Как определить коллинеарность векторов плоскости?

| Оглавление |

Автор: Aлeксaндр Eмeлин