|
Ваш репетитор, справочник и друг!
|
1.8.2. Как определить коллинеарность векторов плоскости?Ортогональность векторов мы проверяли с помощью скалярного произведения, и вот теперь коллинеарность. Для того чтобы два вектора плоскости По существу, это покоординатная детализация очевидного соотношения Задача 37 а) Проверить, коллинеарны ли векторы Решение: а) Выясним, существует ли для векторов И обязательно расскажу о «пижонской» разновидности применения данного правила, которая вполне работает на практике. Идея состоит в том,
чтобы сразу составить пропорцию Отношение можно было составить и наоборот, это равноценный вариант: Для проверки можно использовать тот факт, что коллинеарные векторы линейно выражаются друг через друга. В данном случае
имеют место равенства б) Два вектора плоскости образуют базис, если они не коллинеарны
(линейно независимы). Исследуем на коллинеарность векторы
Из первого уравнения следует, что Вывод: векторы линейно независимы и образуют базис. Упрощённая версия решения выглядит так: Составим пропорцию из соответствующих координат векторов Обычно такой вариант не бракуют рецензенты, но он не применим в тех случаях, когда некоторые координаты равны нулю: Ответ: а) Небольшое творческое задание для самостоятельного решения: Задача 38 При каком значении параметра В образце решения параметр найден через пропорцию Но это ещё не всё. Помимо рассмотренных, существует изящный алгебраический способ проверки векторов на коллинеарность, систематизируем наши знания и пятым пунктом как раз добавим этот способ: Для двух векторов плоскости эквивалентны следующие утверждения: 1) векторы линейно независимы; и, соответственно, эквивалентны следующие противоположные утверждения: ! Проконтролируйте Я очень и очень надеюсь, что на данный момент вы уже эльфы 4-го уровня :) Рассмотрим более подробно новый, пятый пункт: два вектора плоскости Решим Задачу 37 вторым способом: а) Вычислим определитель, составленный
из координат векторов б) Два вектора плоскости образуют базис, если они не коллинеарны. Вычислим определитель, составленный из координат
векторов Ответ: а) Выглядит значительно компактнее и симпатичнее, чем решение с пропорциями. С помощью рассмотренных методов можно устанавливать не только коллинеарность векторов, но и доказывать параллельность отрезков, прямых. Разберём пару задач с конкретными геометрическими фигурами: Задача 39 Даны вершины четырёхугольника Перед доказательством вспомним, что это за геометрическая фигура: параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны (см. Приложение Школьные Материалы).Таким образом, нужно доказать: 1) параллельность противоположных сторон 2) параллельность противоположных сторон Доказываем: 1) Найдём векторы: Вычислим определитель, составленный из координат векторов 2) Найдём векторы: Получился один и тот же вектор («по школьному» – равные векторы), но решение таки лучше
оформить с толком, с расстановкой. Вычислим определитель, составленный из координат векторов Вывод: противоположные стороны четырёхугольника Обратите внимание, что чертёж здесь не нужен – решение чисто аналитическое. Больше фигур хороших и разных: Задача 40 Даны вершины четырёхугольника Это задание для самостоятельного решения. А теперь пора потихонечку перебираться из плоскости в пространство:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»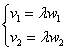 , где
, где 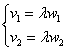 :
: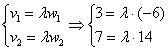
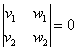 .
.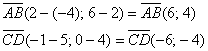
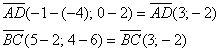
 1.8.3. Как определить коллинеарность векторов пространства?
1.8.3. Как определить коллинеарность векторов пространства? 1.8.1. Базис и система координат на плоскости
1.8.1. Базис и система координат на плоскости