Ваш репетитор, справочник и друг!

Аналитическая геометрия для «чайников»

1.6.7. Как проверить векторы на ортогональность?

Вернёмся к важному случаю, когда векторы являются ортогональными. Напоминаю, что векторы и ортогональны тогда и только тогда, когда . В координатах данный факт запишется следующим образом:
(для векторов плоскости);
(для векторов пространства).

Задача 24

а) Проверить ортогональность векторов: и

б) Выяснить, будут ли перпендикулярными отрезки , если , .

Решение:

а) Выясним, будут ли ортогональны пространственные векторы. Для этого вычислим их скалярное произведение:
, следовательно,

б) Здесь речь идёт об обычных отрезках плоскости. Отрезки обычные, а задача всё равно решается через векторы. Найдём векторы:

и вычислим их скалярное произведение:
, следовательно, векторы и не перпендикулярны, а значит, не перпендикулярны и отрезки .

Ответ: а) , б) отрезки не перпендикулярны.

Задача 25

Даны 4 точки пространства и . Выяснить будут ли перпендикулярными следующие прямые:
а) , б) .

Это задача для самостоятельного решения. По условию требуется проверить перпендикулярность прямых, а решаем снова через векторы – по полной аналогии с предыдущим примером. Геометрически тоже всё очевидно: из ортогональности векторов автоматически следует перпендикулярность соответствующих прямых. Четыре вектора, которые вы найдёте, называют направляющими векторами прямых.

Мощь аналитической геометрии – в векторах

Так, в рассмотренных задачах, с помощью скалярного произведения можно установить не только ортогональность векторов самих по себе, но и перпендикулярность отрезков, прямых. И это приоткрылась только малая часть красоты предмета.

Завершая разговор об ортогональности, разберу ещё одну небольшую задачку, которая время от времени встречается на практике:

Задача 26

При каком значении векторы будут ортогональны?

Решение: по условию требуется найти такое значение параметра , чтобы данные векторы были ортогональны. Два вектора пространства ортогональны тогда и только тогда, когда .

Дело за малым, составим уравнение:

Раскрываем скобки и приводим подобные слагаемые:

Решаем простейшее линейное уравнение:

Ответ: при

Здесь легко выполнить проверку, в исходные векторы подставляем полученное значение параметра :

и находим скалярное произведение:
– да, действительно, при векторы ортогональны, что и требовалось проверить.

Простенький пример для самостоятельного решения:

Задача 27

При каком значении скалярное произведение векторов будет равно –2?
Едем дальше:

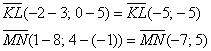
1.6.8. Если векторы заданы суммами векторов с известными координатами

1.6.6. Скалярное произведение векторов в координатах

| Оглавление |

Автор: Aлeксaндр Eмeлин