1.6.8. Если векторы заданы суммами векторов
с известными координатами
Геометрическое масло-масляное:) И мы полакомимся:
Задача 28
Найти скалярное произведение векторов 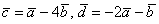 , если , если 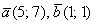 . .
Решение: напрашивается недавняя трафаретная схема, где мы составляли
произведение и раскрывали скобки: 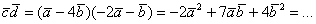 . Но сейчас нам
неизвестны длины векторов . Но сейчас нам
неизвестны длины векторов 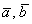 и угол между ними.
Зато известны координаты. И решение на самом деле очень простое. и угол между ними.
Зато известны координаты. И решение на самом деле очень простое.
Найдём вектор 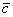 : :
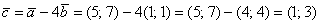
Найдём вектор 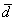 : :
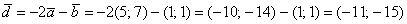
Проделаны элементарные действия с векторами.
Теперь вычислим скалярное произведение:
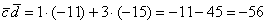
Ответ: 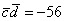
Что и говорить, иметь дело с координатами значительно приятнее.
Задача 29
Найти скалярное произведение векторов 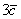 и и 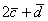 , если , если 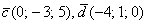
Это пример для самостоятельного решения. И в заключение пункта провокационный пример на вычисление длины вектора:
Задача 30
Найти длины векторов 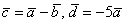 , если , если 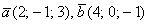
По «горячему» материалу и недавним задачам здесь снова напрашивается путь: 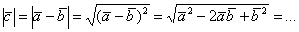 , и да, можно найти длины, скалярное произведение…, но зачем нам эти трудности? , и да, можно найти длины, скалярное произведение…, но зачем нам эти трудности?
Ищите и выбирайте лёгкие решения!
И решение элементарно, найдём вектор 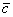 : :
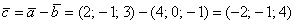
и его длину по тривиальной формуле 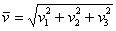 : :
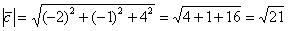
Скалярное произведение здесь вообще не при делах!
Как не при делах оно и при вычислении длины вектора 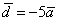 : :
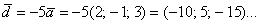 Стоп. А не воспользоваться ли нам очевидным
фактом? Ведь вектор Стоп. А не воспользоваться ли нам очевидным
фактом? Ведь вектор 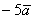 в 5 раз длиннее вектора в 5 раз длиннее вектора 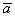 . Направление противоположно, но это не играет роли, ибо разговор о длине. Очевидно,
что длина вектора . Направление противоположно, но это не играет роли, ибо разговор о длине. Очевидно,
что длина вектора 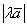 равна произведению модуля
числа равна произведению модуля
числа 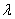 на длину вектора на длину вектора 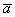 : :
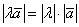 (знак модуля «съедает» возможный минус
числа (знак модуля «съедает» возможный минус
числа 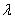 ). ).
Таким образом:
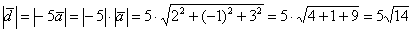
Ответ: 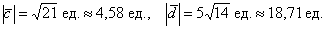
Вот и всё…, всё только начинается!
 1.6.9. Как найти угол между векторами в координатах? 1.6.9. Как найти угол между векторами в координатах?
 1.6.7. Как проверить векторы на ортогональность? 1.6.7. Как проверить векторы на ортогональность?
| Оглавление |
|