|
Ваш репетитор, справочник и друг!
|
1.6.6. Скалярное произведение векторов в координатахПовествование опять пойдёт параллельно – и для векторов плоскости, и для пространственных векторов: Скалярное произведение векторов Скалярное произведение векторов То есть, скалярное произведение равно сумме произведений соответствующих координат векторов. Задача 23 Найти скалярное произведение векторов: а) б) Решение: а) Здесь даны векторы плоскости. По формуле К слову, скалярное произведение получилось отрицательным, а значит,
угол между данными векторами тупой. Пытливые умы могут отложить на плоскости векторы б) А тут речь идёт о точках и векторах пространства. Сначала найдём векторы: Надеюсь, эта простейшая задача у вас уже отработана. По формуле И здесь тоже к слову: скалярное произведение положительно,
следовательно, угол между пространственными векторами Ответ: При некотором опыте скалярное произведение можно приноровиться считать устно. Но лучше письменно, ибо и на старуху бывает
п
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»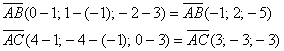
 1.6.7. Как проверить векторы на ортогональность?
1.6.7. Как проверить векторы на ортогональность? 1.6.5. Как найти угол между векторами?
1.6.5. Как найти угол между векторами?