|
Ваш репетитор, справочник и друг!
|
1.9.2. Свойства векторного произведенияНекоторые из них мы уже рассмотрели, но, тем не менее, включу их в данный список. Для произвольных векторов 1) 2) 3) 4) В качестве демонстрации рассмотрим коротенький пример: Задача 48 Найти Решение: по условию снова требуется найти длину векторного произведения. Распишем миниатюру: (1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения. (2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной. (3) Дальнейшее понятно. Ответ: Пора подбросить дров в огонь…, а позже добавим уютную атмосферу и даже сказочных персонажей! – я глубоко убеждён, что высшую математику, тем более геометрию, нельзя излагать сухо и занудно! Задача 49 Вычислить площадь треугольника, построенного на векторах Решение: площадь треугольника рассчитывается по формуле 1) На первом шаге выразим векторное произведение
(1) Подставляем выражения векторов (2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов (каждый член одного многочлена нужно умножить на каждый член другого). (3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2-3 можно выполнять за один шаг. (4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству (5) Приводим подобные слагаемые. В результате вектор оказался выражен через вектор, чего и требовалось достичь: 2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает недавнюю Задачу 48: 3) Найдём площадь искомого треугольника: Ответ: Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения: Задача 50 Найти Посмотрим, насколько вы были внимательны при изучении предыдущих примеров ;-)
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»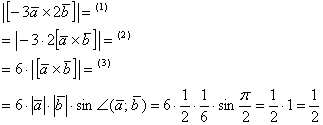
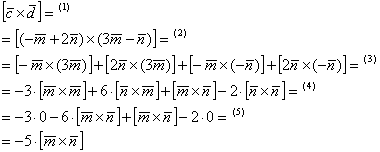
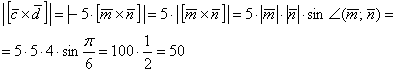
 1.9.3. Векторное произведение в координатах
1.9.3. Векторное произведение в координатах 1.9.1. Векторное произведение векторов. Определение и его смысл
1.9.1. Векторное произведение векторов. Определение и его смысл