|
Ваш репетитор, справочник и друг!
|
1.9.3. Векторное произведение в координатахВекторное произведение векторов В верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов Данный определитель всегда раскрываем по первой строке, что продемонстрировано выше. Что получается в результате раскрытия определителя? В результате получается ВЕКТОР. А как иначе? Векторное произведение – это же вектор: Задача 51 Найти векторное произведение векторов Решение: Задача состоит из двух частей: во-первых, необходимо найти само векторное произведение (вектор), а во-вторых – его длину. 1) Найдём векторное произведение: В результате получен вектор Выполним проверку: по определению, вектор 2) Вычислим длину векторного произведения. Используем простейшую формулу для вычисления длины вектора: Ответ: Аналогичный пример для самостоятельного решения: Задача 52 Даны векторы Будьте внимательны! Огонь камина в самом разгаре, и самое время добавить живительный геометрический смысл в наши задачи: Задача 53 Даны вершины треугольника Решение: Алгоритм решения, думаю, многие уже представляют. Сначала найдём векторы: Затем векторное произведение: Вычислим его длину: Формулы площадей параллелограмма и треугольника, само собой, остаются те же: Ответ: В рассмотренной задаче было не обязательно выбирать стороны Еще одна важная особенность состоит в том, что в задачах на нахождение площади фигуры порядок векторов не имеет значения.
Действительно, если находить Задача 54 Вычислить площадь параллелограмма, построенного на векторах Самостоятельно. Решение и ответ в конце книги. И в заключение параграфа обещанная задача: Задача 55 Проверить, будут ли коллинеарны следующие векторы пространства: а) б) Решение: проверка основана на упомянутом ранее факте: если векторы а) Найдём векторное произведение: Таким образом, векторы б) Найдём векторное произведение: Значит, Ответ: а) не коллинеарны, б) Вот, пожалуй, и все основные сведения о векторном произведении векторов.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»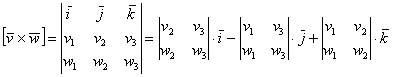
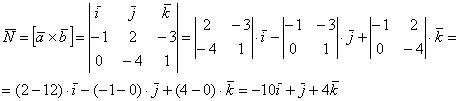
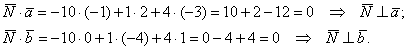
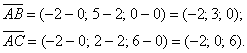
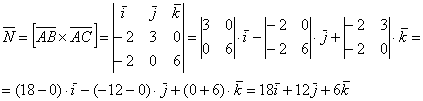
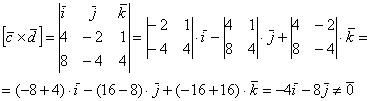
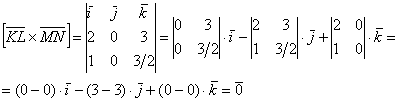
 1.10.1. Смешанное произведение векторов
1.10.1. Смешанное произведение векторов 1.9.2. Свойства векторного произведения
1.9.2. Свойства векторного произведения