1.10.1. Смешанное произведение векторов.
Определение и смысл
Смешанное произведение векторов – это произведение трёх векторов пространства:
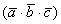
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Определение: смешанным произведением 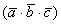 некомпланарных векторов некомпланарных векторов 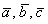 , взятых в данном порядке, называется объём
параллелепипеда, построенного на данных векторах, снабжённый знаком «+», если базис , взятых в данном порядке, называется объём
параллелепипеда, построенного на данных векторах, снабжённый знаком «+», если базис 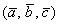 правый, и знаком «–», если базис правый, и знаком «–», если базис 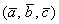 левый. левый.
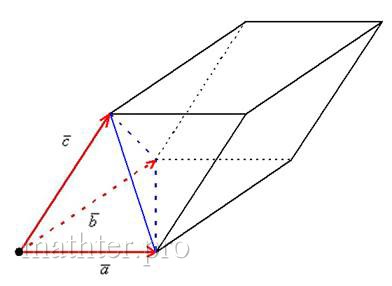
Выполним рисунок, и ниже я снова подробно разберу определение:
1) Исходные векторы 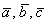 , обозначенные красными стрелками, не компланарны (со случаем компланарности разберёмся отдельно) , обозначенные красными стрелками, не компланарны (со случаем компланарности разберёмся отдельно)
2) Векторы 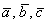 взяты в определённом порядке,
то есть перестановка векторов в произведении взяты в определённом порядке,
то есть перестановка векторов в произведении 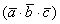 , как вы догадываетесь, не
проходит без последствий. , как вы догадываетесь, не
проходит без последствий.
3) Смешанное произведение векторов является ЧИСЛОМ: 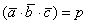 . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через 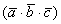 , а результат вычислений буквой «пэ». , а результат вычислений буквой «пэ».
По определению, смешанное произведение – это объём параллелепипеда, построенного на векторах 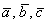 (фигура прочерчена красными векторами и линиями чёрного цвета; невидимые нам линии изображены
пунктиром). То есть, число (фигура прочерчена красными векторами и линиями чёрного цвета; невидимые нам линии изображены
пунктиром). То есть, число 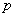 равно объему данного
параллелепипеда. равно объему данного
параллелепипеда.
Примечание: чертёж является схематическим.
4) Не будем заново «париться» с понятием ориентации базиса и пространства. Смысл заключительной части определения состоит в том,
что к объёму 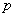 может добавляться знак минус. Простыми словами,
смешанное произведение может быть отрицательным: может добавляться знак минус. Простыми словами,
смешанное произведение может быть отрицательным: 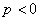 . .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах 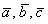 : :
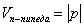
Знак модуля уничтожает возможный «минус» смешанного произведения.
И ещё одна важная формула. В курсе геометрии доказано, что объём тетраэдра (на рисунке отсечён «синей» плоскостью) равен одной шестой
объёма параллелепипеда:
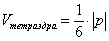
Тетраэдр часто называют треугольной пирамидой, поскольку все грани тетраэдра – треугольники.
Теперь случай компланарности. Если векторы 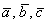 компланарны, то их можно расположить в одной плоскости. В результате параллелепипед «складывается»
в плоскость, и объём такого вырожденного параллелепипеда равен нулю: компланарны, то их можно расположить в одной плоскости. В результате параллелепипед «складывается»
в плоскость, и объём такого вырожденного параллелепипеда равен нулю: 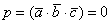 . .
 1.10.2. Как вычислить смешанное произведение? 1.10.2. Как вычислить смешанное произведение?
 1.9.3. Векторное произведение в координатах 1.9.3. Векторное произведение в координатах
| Оглавление |
|