|
Ваш репетитор, справочник и друг!
|
1.10.2. Как вычислить смешанное произведение?Смешанное произведение векторов Утверждение, строго говоря, неполное, но в теоретические тонкости вникать не будем, правоориентированный базис – это «привычный» базис, в котором мы будем решать практические задачи. Вполне достаточно. Как и для векторного произведения, координаты векторов следует «укладывать» в определитель в строгом порядке. Если в смешанном произведении Следует отметить, что координаты векторов не обязательно записывать в строки, их можно записать и в столбцы – слева направо, и тоже в
строгом порядке: Как уже отмечалось, если векторы Закидываем остатки Буратино в огонь: Задача 56 Даны векторы а) смешанное произведение векторов; б) объём параллелепипеда, построенного на векторах в) объём тетраэдра, построенного на векторах Решение прозрачно: а) По формуле смешанного произведения: б) Объём параллелепипеда, построенного на векторах в) Вычислим объём тетраэдра, построенного на данных векторах: Ответ: Следующая задача встречается так часто, что удостаивается отдельного параграфа:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»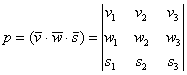
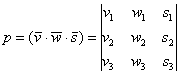 , значение определителя от этого не изменится.
, значение определителя от этого не изменится.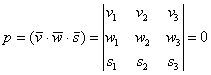
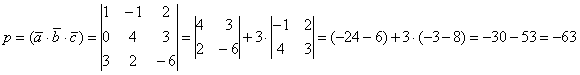
 1.10.3. Как вычислить объём треугольной пирамиды?
1.10.3. Как вычислить объём треугольной пирамиды? 1.10.1. Смешанное произведение векторов
1.10.1. Смешанное произведение векторов