1.10.3. Как вычислить объём треугольной пирамиды?

или тетраэдра, …только что решали, но тут другое, типовое условие:

Задача 57

Вычислить объём треугольной пирамиды, если даны её вершины

Решение: «чайникам» рекомендую выполнить схематический рисунок пирамидки, чтобы лучше понять суть проводимых действий.

Сначала найдём векторы:

Вычислим смешанное произведение:

(определитель раскрыт по первой строке)

Вычислим объём треугольной пирамиды :

Ответ:

Рассмотренная задача имеет не единственное решение, можно было взять и другую группу векторов, начиная «движуху» от любой другой вершины пирамиды (итого 4 варианта). Чем-то похоже на Задачу 53 о площади треугольника, где мы могли выбрать любую из трёх вершин.

Объём тетраэдра – это «хит» смешанного произведения, поэтому заключительное задание пусть будет таким же:

Задача 58

Вычислить объём пирамиды, заданной вершинами ,

В образце решения я рассмотрел векторы от «традиционной» точки , но ради исследовательского интереса вы можете выбрать любую другую вершину. Результаты должны совпасть. Напоминаю, что для к книге приложены Алгебраический и Геометрический Калькулятор. Они практически 100%-но позволят вам не пропустить вычислительную ошибку.

Точно так же как у скалярного и векторного, у смешанного произведения есть свои свойства, и о некоторых из них я рассказал в начале параграфа; другие же не имеют особого значения для «массовой» практики, и если они вам нужны, пожалуйста, обратитесь к учебной литературе.

Остались только веселящие душу угольки, и повод для радости действительно есть! – ведь Главу о векторах удалось уместить всего лишь на 60 страницах, чего не ожидал даже я сам. Для такого объёма информация, пожалуй, рекорд.

И в заключение Главы важное напутствие:

Любите векторы, и векторы полюбят вас!

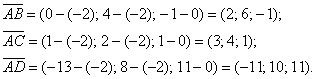
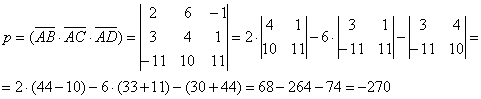
2.1. Уравнение прямой с угловым коэффициентом

1.10.2. Как вычислить смешанное произведение?

| Оглавление |

Автор: Aлeксaндр Eмeлин