2.1. Уравнение прямой с угловым коэффициентом
Прямая – это одна из простейших геометрических фигур. Она бесконечна:

и обозначается маленькими латинскими буквами 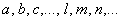 , как вариант, , как вариант,
с подстрочным индексом, например, 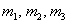 . Также прямую можно обозначить двумя различными точками, которые ей принадлежат, например, . Также прямую можно обозначить двумя различными точками, которые ей принадлежат, например, 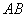 . .
Прямую часто задают уравнением, и начнём мы опять со школьного материала. Всем известное «школьное» уравнение 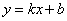 называется уравнением прямой с угловым коэффициентом называется уравнением прямой с угловым коэффициентом 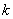 . Вспомним геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой: . Вспомним геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой:
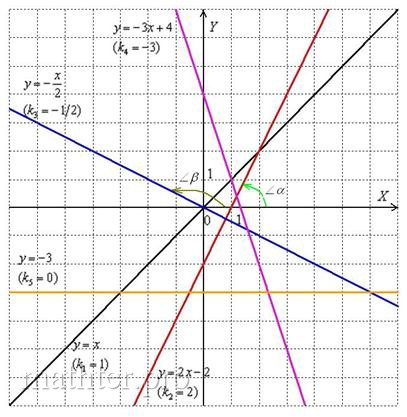
Угловой коэффициент прямой равен тангенсу угла (см. Приложение Тригонометрия) между положительным направлением оси 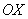 и данной прямой: и данной прямой: 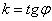 . Чтобы не загромождать чертёж, я нарисовал углы только для двух прямых: . Чтобы не загромождать чертёж, я нарисовал углы только для двух прямых:
Это «красная» прямая 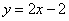 с коэффициентом с коэффициентом 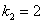 . Согласно вышесказанному, . Согласно вышесказанному, 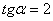 (угол «альфа» обозначен зелёной дугой). Для «синей» прямой (угол «альфа» обозначен зелёной дугой). Для «синей» прямой 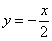 с с 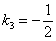 справедливо равенство справедливо равенство 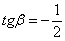 (угол «бета» обозначен коричневой дугой). (угол «бета» обозначен коричневой дугой).
Если известен тангенс угла, то при необходимости легко найти и сам угол с помощью обратной функции – арктангенса. Так, для «черной» прямой 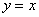 тангенс угла наклона равен тангенс угла наклона равен 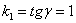 , а сам угол наклона составляет: , а сам угол наклона составляет:
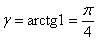 радиан или 45 градусов, что хорошо видно по чертежу. Значения углов можно находить по Таблице или с помощью Калькулятора (Приложения в помощь). радиан или 45 градусов, что хорошо видно по чертежу. Значения углов можно находить по Таблице или с помощью Калькулятора (Приложения в помощь).
Таким образом, угловой коэффициент характеризует степень наклона прямой к оси абсцисс. При этом возможны следующие случаи:
1) Если угловой коэффициент отрицателен: 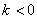 , то линия, грубо говоря, идёт «сверху вниз». Примеры – «синяя» и «малиновая» прямые на чертеже. , то линия, грубо говоря, идёт «сверху вниз». Примеры – «синяя» и «малиновая» прямые на чертеже.
2) Если угловой коэффициент положителен: 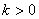 , то линия идёт «снизу вверх». Примеры – «чёрная» и «красная» прямые на чертеже. , то линия идёт «снизу вверх». Примеры – «чёрная» и «красная» прямые на чертеже.
3) Если угловой коэффициент равен нулю: 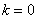 , то уравнение , то уравнение 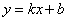 принимает вид принимает вид 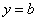 , и соответствующая прямая параллельна оси , и соответствующая прямая параллельна оси 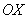 . Пример – «жёлтая» прямая. Неформальный смысл уравнения: «игрек» ВСЕГДА (при любом «икс») равен «бэ». . Пример – «жёлтая» прямая. Неформальный смысл уравнения: «игрек» ВСЕГДА (при любом «икс») равен «бэ».
4) Для семейства прямых 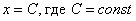 , параллельных оси , параллельных оси 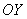 (на чертеже нет примера, кроме самой оси (на чертеже нет примера, кроме самой оси 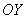 ), угловой коэффициент не определён. В данной ситуации ), угловой коэффициент не определён. В данной ситуации 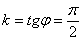 , а тангенса угла 90 градусов не существует. Неформальный смысл уравнения: «икс» ВСЕГДА (при любом «игрек») равен «цэ». , а тангенса угла 90 градусов не существует. Неформальный смысл уравнения: «икс» ВСЕГДА (при любом «игрек») равен «цэ».
Чем больше угловой коэффициент по модулю, тем круче идёт график прямой.
Рассмотрим прямые 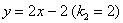 и и 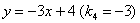 . Здесь . Здесь 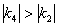 , поэтому прямая , поэтому прямая 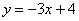 имеет более крутой наклон. Напоминаю, что модуль позволяет не учитывать знак, нас интересуют только абсолютные значения угловых коэффициентов. имеет более крутой наклон. Напоминаю, что модуль позволяет не учитывать знак, нас интересуют только абсолютные значения угловых коэффициентов.
В свою очередь, прямая 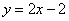 более крутА, чем прямые более крутА, чем прямые 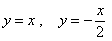 . .
Обратно: чем меньше угловой коэффициент по модулю, тем прямая является более пологой. Так, для прямых 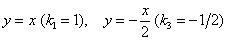 справедливо неравенство справедливо неравенство 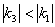 , таким образом, прямая , таким образом, прямая 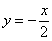 более пологая. более пологая.
Зачем эта информация? Продлить ваши мучения. Знания вышеперечисленных фактов позволяет немедленно увидеть свои ошибки, в частности, ошибки при построении графиков – когда на чертеже получилось явно «что-то не то». Желательно, чтобы вам сразу было понятно, что прямая 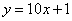 весьма крутА и идёт «снизу вверх», а прямая весьма крутА и идёт «снизу вверх», а прямая 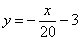 – очень полога, близко прижата к оси – очень полога, близко прижата к оси 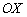 и идёт «сверху вниз». и идёт «сверху вниз».
Сомневался, напоминать ли, но на всякий пожарный: как построить прямую, если известно её уравнение?
Для того чтобы построить прямую, нужно знать две её точки (любые). Их легко найти из уравнения. Рассмотрим, например, уравнение 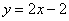 и выберем произвольное значение «икс», удобно взять и выберем произвольное значение «икс», удобно взять 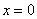 , тогда: , тогда: 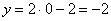 , и первая точка найдена: , и первая точка найдена: 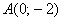 . Теперь выбираем другое значение . Теперь выбираем другое значение 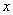 , например, , например, 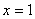 и находим и находим 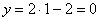 – точка – точка 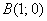 . Отмечаем точки на чертеже и аккуратно проводим линию по линейке. . Отмечаем точки на чертеже и аккуратно проводим линию по линейке.
Ах да, чуть не забыл: прямая вида 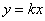 называется прямой пропорциональностью. Она проходит через начало координат, и для её построения достаточно найти одну точку. На чертеже выше изображены две таких прямых + ось называется прямой пропорциональностью. Она проходит через начало координат, и для её построения достаточно найти одну точку. На чертеже выше изображены две таких прямых + ось 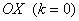 . .
Как составить уравнение прямой с угловым коэффициентом?
Если известна точка 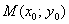 , принадлежащая некоторой прямой, и угловой коэффициент , принадлежащая некоторой прямой, и угловой коэффициент 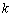 этой прямой, то уравнение данной прямой выражается формулой: этой прямой, то уравнение данной прямой выражается формулой:
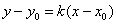
Задача 59
Составить уравнение прямой с угловым коэффициентом 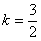 , если известно, что точка , если известно, что точка 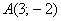 принадлежит данной прямой. принадлежит данной прямой.
Решение: уравнение составим по формуле 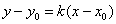 . В данном случае: . В данном случае:
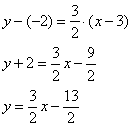
Ответ: 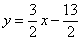
Проверка выполняется элементарно. Во-первых, смотрим на полученное уравнение 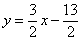 и убеждаемся, что наш угловой коэффициент и убеждаемся, что наш угловой коэффициент 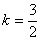 на своём месте. Во-вторых, координаты точки на своём месте. Во-вторых, координаты точки 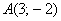 должны удовлетворять данному уравнению. Подставим их в уравнение: должны удовлетворять данному уравнению. Подставим их в уравнение:
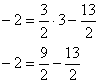
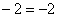 – получено верное равенство, значит, точка – получено верное равенство, значит, точка 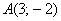 удовлетворяет полученному уравнению. удовлетворяет полученному уравнению.
Вывод: уравнение найдено правильно.
Более хитрая задачка для самостоятельного решения:
Задача 60
Составить уравнение прямой, если известна её точка 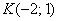 , а угол наклона к положительному направлению оси , а угол наклона к положительному направлению оси 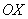 составляет составляет 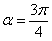 . .
Ну что же, прозвенел «последний звонок», отгремел выпускной бал (как это быстро у меня происходит :)), и за воротами родной школы нас поджидает, собственно, аналитическая геометрия:
 2.2.1. Общее уравнение и направляющий вектор прямой 2.2.1. Общее уравнение и направляющий вектор прямой
 1.10.3. Как вычислить объём треугольной пирамиды? 1.10.3. Как вычислить объём треугольной пирамиды?
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»

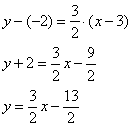
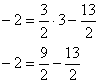
 2.2.1. Общее уравнение и направляющий вектор прямой
2.2.1. Общее уравнение и направляющий вектор прямой 1.10.3. Как вычислить объём треугольной пирамиды?
1.10.3. Как вычислить объём треугольной пирамиды?