3. Многочлены
Многочлены, многочлены, многочлены – учат в школе, учат в школе, учат в школе. И мы их не только повторим, но и приправим высшей алгеброй :) Во-первых, у этого понятия есть синоним: полином. И во-вторых, за ним где-то робко прячется одночлен.
Одночлен – это произведение, состоящее из числовых множителей и переменных в целых неотрицательных степенях, например: 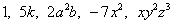 и так далее. Как видите, «одинокая» константа (любое число) тоже считается одночленом. и так далее. Как видите, «одинокая» константа (любое число) тоже считается одночленом.
Сумму степеней при различных переменных называют степенью одночлена, так 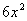 – одночлен 2-й степени, – одночлен 2-й степени, 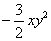 – одночлен 1 + 2 = 3-й степени и – одночлен 1 + 2 = 3-й степени и 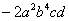 – одночлен 2 + 4 + 1 + 1 = 8-й степени. Степень константы – одночлен 2 + 4 + 1 + 1 = 8-й степени. Степень константы 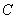 («цэ большое») равна нулю. («цэ большое») равна нулю.
Если в произведении есть что-то ещё (корни, нечисловые дроби, другие функции), или другие действия, то это уже не одночлен: 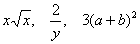 . Это просто член. . Это просто член.
Многочленом называют сумму одночленов, например: 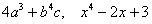 , причём первый также величают двучленом, а второй – трёхчленом. По количеству одночленов. Степень многочлена – это максимальная степень входящих в него одночленов. Так, первый многочлен имеет 5-ю степень (4 + 1), а второй – 4-ю степень. , причём первый также величают двучленом, а второй – трёхчленом. По количеству одночленов. Степень многочлена – это максимальная степень входящих в него одночленов. Так, первый многочлен имеет 5-ю степень (4 + 1), а второй – 4-ю степень.
В частности, многочленом считают и любой одночлен, к нему всегда можно приписать нулевые слагаемые: 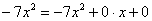 . Это важный технический приём, используемый в некоторых задачах. . Это важный технический приём, используемый в некоторых задачах.
Многочлены встретились нам не только в школьной программе, но и в курсе аналитической геометрии. Так, в уравнении линии второго порядка, приведу общее уравнение: 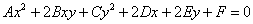 – в левой части находится многочлен двух переменных. А уравнения поверхностей, например – в левой части находится многочлен двух переменных. А уравнения поверхностей, например 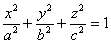 , содержат многочлены трех переменных. Переменных, разумеется, может быть и больше, и даже очень много, но сейчас нас будут интересовать многочлены одной переменной. , содержат многочлены трех переменных. Переменных, разумеется, может быть и больше, и даже очень много, но сейчас нас будут интересовать многочлены одной переменной.
Многочлен одной переменной 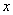 – это выражение вида: – это выражение вида:
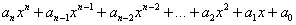 , где , где 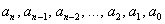 – числовые коэффициенты, причём, – числовые коэффициенты, причём, 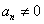 . Коэффициенты могут быть целыми или рациональными или действительными или комплексными. Это как мы решим сами. Но чаще за нас :) . Коэффициенты могут быть целыми или рациональными или действительными или комплексными. Это как мы решим сами. Но чаще за нас :)
Натуральное число 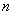 называют степенью многочлена, а коэффициент называют степенью многочлена, а коэффициент 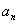 – старшим коэффициентом. Коэффициент – старшим коэффициентом. Коэффициент 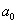 называется свободным членом. называется свободным членом.
Многочлен вида 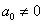 имеет нулевую степень, его можно ещё записать так: имеет нулевую степень, его можно ещё записать так: 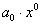 , а если эта константа – ноль, то перед нами нулевой многочлен. Его степень не определена. И в самом деле, к нулю можно добавить сколько хочешь нулевых одночленов: , а если эта константа – ноль, то перед нами нулевой многочлен. Его степень не определена. И в самом деле, к нулю можно добавить сколько хочешь нулевых одночленов: 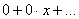
Примечание: в некоторых источниках, моих в том числе, используется реверсное обозначение коэффициентов 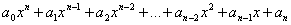 . Это эквивалентный, но менее удобный вариант. . Это эквивалентный, но менее удобный вариант.
 3.1. Сложение и умножение многочленов 3.1. Сложение и умножение многочленов
 2.3. Уравнения с комплексными числами 2.3. Уравнения с комплексными числами
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих 3.1. Сложение и умножение многочленов
3.1. Сложение и умножение многочленов 2.3. Уравнения с комплексными числами
2.3. Уравнения с комплексными числами