Ваш репетитор, справочник и друг!

Высшая алгебра для начинающих

2.3. Уравнения с комплексными числами

Некоторые из них нам уже встретились ранее:

Повторим школьный материал. Уравнение – это равенство, которое содержит переменную (либо переменные). В нашей теме речь идёт о комплексной переменной «зет». Любое уравнение состоит из левой части, правой части и знака «равно».

Корень уравнения – это ТАКОЕ значение переменной, которое обращает уравнение в верное числовое равенство. Решить уравнение – это значит найти ВСЕ его корни или доказать, что их не существует.

Так, квадратное уравнение , как мы выяснили, имеет два комплексных корня (которые в частности могут оказаться действительными). Уравнение вида имеет ровно комплексных корней, и технически его решение – есть извлечение корня «энной» степени из числа «дубльвэ.

Для уравнений с комплексной переменной справедливы те же равносильные преобразования, что и для «обычных» уравнений (такие преобразования никак не затрагивают корни). В частности, слагаемые можно переносить из части в часть со сменой знака:

Следует сказать, что слагаемЫМИ тут формально можно считать и :
, однако всегда нужно помнить, что – это единое число, а не сложение!

Обе части уравнения можно умножить / разделить на одно и то же комплексное число, отличное от нуля. Рассмотрим простенькое уравнение . Для разрешения этого уравнения относительно «зет», нужно разделить обе его части на или, что академичнее – умножить на :

Теперь выполняем деление. Для этого нужно умножить числитель и знаменатель на сопряжённое знаменателю число:

– корень уравнения.

Выполним проверку, для этого подставим найденное значение в левую часть исходного уравнения: – в результате получена правая часть, значит, корень найден верно. Эквивалентно можно сказать, что при подстановке в уравнение значения получено верное числовое равенство:
Возможно, следующие примеры некоторым покажутся экзотическими, но я ничего не придумываю – все они взяты из ваших реальных работ:

Пример 25

Решить уравнение

Решение, в принципе, можно оформить пошагово, но в данном случае овчинка выделки не стОит. На первом шаге нужно упростить всё, что не содержит неизвестной «зет», в результате чего уравнение сведётся к виду .
Уверенно упрощаем среднюю дробь, домножая числитель и знаменатель на сопряженное знаменателю число:

Полученный результат* переносим в правую часть со сменой знака:

* Примечание: обращаю внимание, что полученный результат – это не комплексное число, а частное двух чисел ( и 13). Следует заметить, что дробь легко преобразовать в комплексное число: , но тогда и с дробью правой части нужно сделать то же самое: . В этом случае после переноса числа в правую часть речь пойдёт о разности двух чисел: .

Ну а в текущем контексте мы подводим дроби под единый знаменатель и упрощаем числитель:

Выполняем деление в правой части, приводя уравнение к виду :

И здесь мы встречаемся ещё с одним равносильным преобразованием уравнения – его я условно назвал правило пропорции и напоминаю «на пальцах»: ненулевой множитель можно перенести из числителя одной части – в знаменатель другой. И наоборот.

Итак, по правилу пропорции, выражаем «зет» из , держа в уме, что оно не может равняться нулю: . Части уравнения меняем местами:

Теперь можно снова выполнить деление, но подозрительно похожие числа числителя и знаменателя подсказывают хитрый ход – вынесение мнимой единицы за скобки с последующим сокращением одинаковых чисел:

Проверка: подставим полученное значение в левую часть исходного уравнения и проведём упрощения:

– получена правая часть исходного уравнения, таким образом, действительно является корнем уравнения.

Ответ:

…Сейчас-сейчас…, подберу для вас что-нибудь поинтереснее…, держите:

Пример 26

Решить уравнение , выполнить проверку.

Это уравнение, очевидно, сводится к линейному , курс определён, дерзайте!

И в заключение параграфа «добьём» квадратное уравнение . Помимо комплексных корней, у него могут быть ещё и комплексные коэффициенты:

Пример 27

Найти корни уравнения .

Квадратное уравнение с комплексными коэффициентами тоже всегда имеет два корня и решается по такой же схеме, что и «обычное» квадратное уравнение с некоторыми отличиями в технике вычислений.

Во-первых, обратим внимание на коэффициент . От мнимой единицы, в принципе, можно избавиться (умножив обе части уравнения на ), однако в этом нет особой надобности.

Для удобства выпишем коэффициенты:
– не теряем «минус» у свободного члена!
…Обозначения, конечно, не сильно удобные – с подстрочными индексами, но я стараюсь придерживаться канонов, с которыми вы встретитесь в других источниках.

Вычислим дискриминант:
А вот и главное препятствие:

Применение общей формулы извлечения корня осложняется серьёзными затруднениями, связанными с аргументом подкоренного комплексного числа (убедитесь сами). Но существует и другой, алгебраический путь! Корень будем искать в виде:

Возведём обе части уравнения в квадрат:

Два комплексных числа равны, если равны их действительные и их мнимые части соответственно. Таким образом, получаем следующую систему:

Попытаем счастья решить систему подбором (более основательный путь – выразить из 2-го уравнения – подставить в 1-е, получить и решить биквадратное уравнение). Предполагая, что автор задачи не изверг, выдвигаем гипотезу, что и – целые числа. Из положительной разности (1-го уравнения) следует, что «икс» по модулю (см. Приложение Горячие формулы) больше, чем «игрек». Кроме того, положительное произведение сообщает нам, что неизвестные одного знака (оба положительны либо оба отрицательны). Исходя из вышесказанного, и ориентируясь на 2-е уравнение, запишем все подходящие ему пары целых значений:

Устной подстановкой выясняем, что 1-му уравнению системы удовлетворяют две последние пары, таким образом:

Не помешает промежуточная проверка:
– подкоренное число, и очевидно:
, что и требовалось проверить.

В качестве «рабочего» корня можно выбрать как число , так и . Понятно, что лучше взять версию без «минусов»:

Находим корни, не забывая, кстати, что :

Проверим, удовлетворяют ли найденные значения уравнению :

1) Подставим :

– верное равенство.

2) Подставим :

– верное равенство.

Таким образом, действительно являются корнями данного уравнения.

Ответ:

По мотивам разобранной задачи примеры для самостоятельного решения:

Пример 28

Найти корни уравнения

Следует заметить, что квадратный корень из чисто комплексного числа прекрасно извлекается и с помощью общей формулы , где , поэтому в образце приведены оба способа. Второе полезное замечание касается того, что предварительное извлечение корня из константы ничуть не упрощает решение.

А теперь можно расслабиться – в этом примере вы отделаетесь лёгким испугом :)

Пример 29

Решить уравнение и выполнить проверку.

Решения и ответы в конце книги.

И я вас поздравляю с успешным (надеюсь) освоением темы!

Глава закончилась, но комплексные числа – вовсе нет!

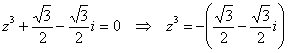
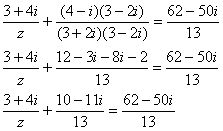
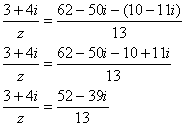
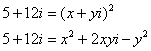
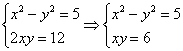
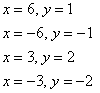
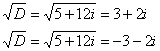
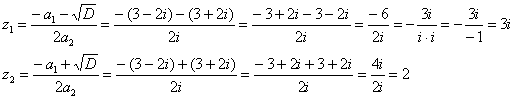
3. Многочлены

2.2. Выражения с комплексными числами

| Оглавление |

Автор: Aлeксaндр Eмeлин