|
Ваш репетитор, справочник и друг!
|
2.1.4. Тригонометрическая форма комплексного числаДо сих пор мы имели дело с алгебраической формой комплексного числа, но есть альтернатива. Любое
комплексное число (кроме нуля)
Не тушуемся, всё проще, чем кажется. Изобразим на комплексной плоскости число Модулем комплексного числа Модуль комплексного числа По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: Аргументом комплексного числа Аргумент не определён для единственного числа: Аргумент комплексного числа И из геометрических соображений получается следующая формула для нахождения аргумента: Но сначала рассмотрим простейшие примеры, когда комплексные числа располагаются на координатных осях: Пример 7 Представить в тригонометрической форме комплексные числа: Выполним чертёж, хотя на самом деле задание устное: Для наглядности перепишу
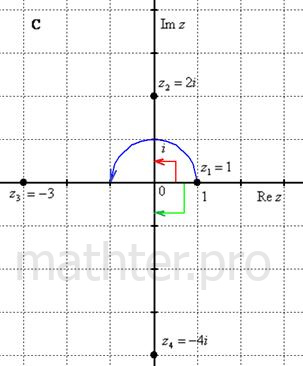
тригонометрическую форму комплексного числа: 1) Представим в тригонометрической форме число Ясно, как день, обратное проверочное действие: 2) Представим в тригонометрической форме число Используя Таблицу значений тригонометрических функций (см. Приложение Тригонометрические таблицы) легко
обратно получить алгебраическую форму числа (заодно выполнив проверку): 3) Представим в тригонометрической форме число И понятно, что Проверка: 4) И четвёртый интересный случай. Представим в тригонометрической форме число А вот аргумент можно записать разными способами. Во-первых, напрашивается выбрать значение Проверка: Однако более стандартно следующее правило: если угол больше 180 градусов, то его записывают со знаком минус и
противоположной ориентацией («прокруткой») угла: Таким образом, запись принимает вид: ! Причём здесь ни в коем случае нельзя использовать четность косинуса,
нечетность синуса и проводить дальнейшее «упрощение» записи: Задание выполнено. В оформлении простейших примеров так и следует записывать: «Очевидно, что модуль равен…,Очевидно, что аргумент равен...». Ибо это действительно очевидно и легко решается устно. Перейдем к рассмотрению более распространенных случаев:
Как я уже отмечал, с модулем проблем не возникает, всегда следует использовать формулу 1) если 2) если 3) если Пример 8 Представить в тригонометрической форме комплексные числа: Коль скоро в нашем распоряжении есть готовые формулы, то чертеж выполнять не обязательно. Но есть один момент: когда вам предложено такое
задание, то чертёж лучше в любом случае выполнить. Во-первых, для контроля правильности решения, и во-вторых его частенько требуют
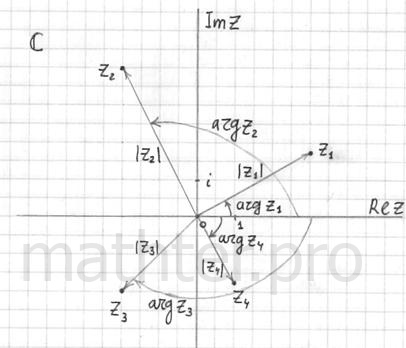
преподаватели. Полагаю, ручное оформление решения будет в ходу ещё долго, поэтому немного живописи: Я представлю в тригонометрической форме числа Представим в тригонометрической форме число Расскажу о самобытном способе проверки. Если вы будете выполнять чертеж на клетчатой бумаге в том масштабе, который у меня (1 ед. = 1 см), то можно взять линейку и измерить модуль в сантиметрах. Если есть транспортир, то непосредственно по чертежу можно измерить и угол. Перечертите чертёж в тетрадь и измерьте линейкой расстояние от начала координат до числа Представим в тригонометрической форме число Итак: А вот здесь, как уже отмечалось, минусы не трогаем. Помимо забавного графического метода проверки, не забываем и о проверке аналитической, которая уже проводилась ранее. Используем Таблицу значений тригонометрических функций, при этом учитываем, что угол Числа Краткое решение и ответы в конце книги.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих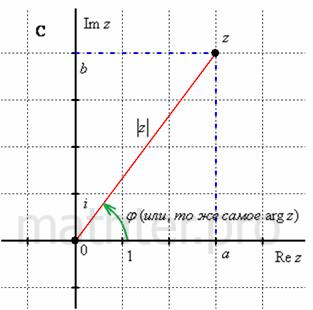
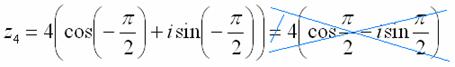
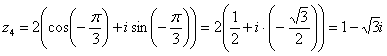 – число
– число  2.1.5. Показательная форма комплексного числа
2.1.5. Показательная форма комплексного числа 2.1.3. Деление комплексных чисел
2.1.3. Деление комплексных чисел