2.1.3. Деление комплексных чисел

Для выполнения этого действия нам понадобится понятие сопряжённого комплексного числа. Число называют сопряжённым для числа (и наоборот). Таким образом, – это пара сопряженных (по отношению друг к другу) чисел.

Пример 4

Даны комплексные числа , . Найти частное .

Решение: составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю число.

Смотрим на наш знаменатель: . В знаменателе находится число вида , поэтому сопряженным для него является , то есть .

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Зачем это нужно? Чтобы воспользоваться эпичной формулой разности квадратов , избавившись тем самым от мнимой единицы в знаменателе. Ну а в числителе просто раскрываем скобки (умножаем числа). Распишу подробно:

Помним, что и не путаемся в знаках!!!

ПризнАюсь, пример я подобрал «хороший», если взять два числа «от фонаря», то в результате деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:

Редко, но встречается такое задание:

Пример 5

Дано комплексное число . Записать данное число в алгебраической форме (т. е. в форме ).

Решение: приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю число. В знаменателе у нас число с «плюсом» посредине: , поэтому сопряжённым для него будет число с «минусом»: . Таким образом, числитель и знаменатель нужно умножить на , чтобы воспользоваться формулой и избавиться от в знаменателе:
– исходное число в алгебраической форме. Обращаю внимание, что это одно и то же число!

Пример 6

Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.

Это пример для самостоятельного решения. Образец для сверки в конце книги.

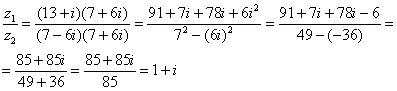
2.1.4. Тригонометрическая форма комплексного числа

2.1.2. Умножение комплексных чисел

| Оглавление |

Автор: Aлeксaндр Eмeлин