Ваш репетитор, справочник и друг!

Высшая алгебра для начинающих

1.2.8. Эквиваленция. Необходимое и достаточное условие

Эквиваленция обозначается значком и читается «тогда и только тогда»

И, наверное, многие догадываются, что это за операция: эквиваленцией высказываний и называют высказывание , которое истинно в том и только том случае, когда высказывания и истинны или ложны одновременно:

Данная операция естественным образом выражается формулой – «из а следует бэ и из бэ следует а». Предположим, что Петя вышел на финишную черту сессии, и ему осталось сдать 3 экзамена. Рассмотрим высказывания:
– три экзамена сданы, – сессия успешно завершена.

Очевидно, что при описанных выше обстоятельствах эти высказывания эквиваленты: – сессия успешно завершена тогда и только тогда, когда сдано 3 экзамена.

И это пример необходимого и достаточного условия: для того чтобы завершить сессию успешно Пете необходимо сдать 3 экзамена (в противном случае сессия будет не сдана) и в то же самое время этого достаточно (т. к. больше ничего делать не нужно).

Особенность эквиваленции состоит в том, что имеет место либо и то и другое, либо ничего, например:
Петя занимается штангой тогда и только тогда, когда Маша вяжет варежки

Это означает, что либо Петя занимается штангой и Маша вяжет варежки, либо они оба лежат на диване. Причём связка «тогда и только тогда» понимается очень жёстко: как только Петя взял в руки штангу, так сразу Маша – спицы, и наоборот, если Маша вяжет варежки, то Петя непременно качается штангой.

Вот в чём сила необходимого и достаточного условия! – оно объединяет и дисциплинирует =) Прочувствуйте отличие от фразы «Если Петя качается, то Маша вяжет» ;)

К слову, о дисциплине: рациональный подход как раз и предполагает необходимость и достаточность – когда человек для достижения какой-либо цели делает ровно столько, сколько нужно, и не больше. Это, конечно, бывает скучно в обычной жизни, но всячески приветствуется в математических рассуждениях, которые нас уже заждались:

Треугольник является равносторонним тогда и только тогда, когда у него равные углы

Высказывания – треугольник равносторонний и – у него равные углы можно соотнести эквиваленцией , но на практике мы почти всего связываем их обоюдоострым значком логического следствия , который тоже читается «тогда и только тогда». Отличие от эквиваленции такое же – когда мы утверждаем, что , то изначально полагаем высказывание истиной (и никак не ложью). И наоборот, запись подразумевает безусловную истинность посылки .

И в заключение параграфа вспомним знаменитую теорему, которую я переформулирую «по-взрослому»:

Для того, что треугольник был прямоугольным необходимо и достаточно, чтобы квадрат одной из его сторон равнялся сумме квадратов двух других сторон: .
Справка: напоминаю, что сторона называется гипотенузой (бОльшая сторона, лежащая напротив угла ), а стороны – катетами.

Перепишем теорему в сокращённой записи:
– треугольник прямоугольный – выполнено

Доказательство теорем такого типа состоит из двух частей, у которых тоже есть стандартные названия (наверное, неоднократно сталкивались):

1) Необходимость (условия ).
– иными словами, здесь нужно доказать, что для того, чтобы треугольник был прямоугольным, необходимо выполнение равенства .

Данный пункт – это собственно и есть теорема Пифагора, формулировка которой нам знакома ещё со школы: «Если треугольник прямоугольный, то ».

2) На втором шаге обосновывается достаточность:
– здесь надо доказать, что справедливость равенства достаточна для того, чтобы треугольник был прямоугольным.

Учащихся опять же такими словами не запугивают, и второй пункт формулируют в виде обратной теоремы Пифагора: «Если , то треугольник прямоугольный».

Связей по схеме «тогда и только тогда» в математике тьма, и я только что привёл стандартную схему их доказательства. И, конечно же, всегда анализируйте, что означают «необходимо», «достаточно», «необходимо и достаточно» в том или ином случае.

Следует отметить, что теорему можно рассмотреть с точки зрения логической операции , но вот импликация (как и обратная запись ) становится нелегальной! Почему? Пусть – треугольник не прямоугольный, – равенство выполнено. Но тогда по импликационной таблице получаем , что не соответствует действительности!

Но зато записи совершенно законны, поскольку логическое следствие отталкивается исключительно от истины! Вот она в чём тонкость.

Математическая логика формальна (повторюсь), и это отдельный раздел математики, со своими формулами, законами, теоремами и т. д. Но для дальнейшего изучения алгебры (да и не только её) информации вполне достаточно, и жду вас в следующей теме, после того, как мы немного расширим свой кругозор:

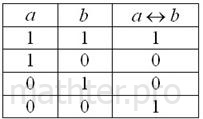
1.3. Понятие алгебраической структуры. Примеры

1.2.7. Логическое следствие

| Оглавление |

Автор: Aлeксaндр Eмeлин